本题共有2个小题,第 1小题满分6分,第2小题满分10分.
1小题满分6分,第2小题满分10分.
某火山喷发停止后,为测量的需要,设距离喷口中心 米内的圆环面为第
米内的圆环面为第 区、
区、 米至
米至 米的圆环面为第
米的圆环面为第 区、……、第
区、……、第 米至
米至 米的圆环面为
米的圆环面为 第
第 区,…,现测得第
区,…,现测得第 区火山灰平均每平方米为1000千克、第
区火山灰平均每平方米为1000千克、第 区每平方米的平均重量较第
区每平方米的平均重量较第 区减少
区减少 、第
、第 区较第
区较第 区又减少
区又减少
 ,以此类推,求:
,以此类推,求:
(1)离火山口1225米处的圆环面平均每平方米火山灰重量(结果精确到1千克)?
(2)第几区内的火 山灰总重量最大?
山灰总重量最大?
已知圆 的方程为
的方程为 ,直线
,直线
 ,设点
,设点 .
.
(1)若点 在圆
在圆 外,试判断直线
外,试判断直线 与圆
与圆 的位置关系;
的位置关系;
(2)若点 在圆
在圆 上,且
上,且 ,
, ,过点
,过点 作直线
作直线 分别交圆
分别交圆 于
于 两点,且直线
两点,且直线 和
和 的斜率互为相反数;
的斜率互为相反数;
① 若直线 过点
过点 ,求
,求 的值;
的值;
② 试问:不论直线 的斜率怎样变化,直线
的斜率怎样变化,直线 的斜率是否为定值?若是,求出该定值;若不是,说明理由.
的斜率是否为定值?若是,求出该定值;若不是,说明理由.
设 是数列
是数列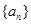 的前
的前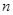 项和,且
项和,且 .
.
(1)当 ,
, 时,求
时,求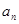 ;
;
(2)若数列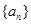 为等差数列,且
为等差数列,且 ,
,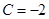 .
.
①求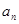 ;
;
②设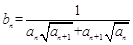 ,且数列
,且数列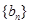 的前
的前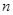 项和为
项和为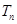 ,求
,求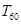 的值.
的值.
为绘制海底地貌图,测量海底两点 ,
, 间的距离,海底探测仪沿水平方向在
间的距离,海底探测仪沿水平方向在 ,
, 两点进行测量,
两点进行测量, ,
, ,
, ,
, 在同一个铅垂平面内. 海底探测仪测得
在同一个铅垂平面内. 海底探测仪测得


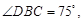
 ,
, 两点的距离为
两点的距离为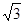 海里.
海里.
(1)求 的面积;
的面积;
(2)求 ,
, 之间的距离.
之间的距离.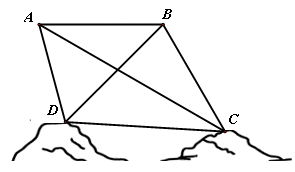
(本小题满分14分)在四边形 中,已知
中,已知 ,
, ,
, .
.
(1)若四边形 是矩形,求
是矩形,求 的值;
的值;
(2)若四边形 是平行四边形,且
是平行四边形,且 ,求
,求 与
与 夹角的余弦值.
夹角的余弦值.
已知函数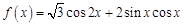 ,
, .
.
(1)求函数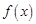 的最小正周期;
的最小正周期;
(2)求函数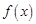 在区间
在区间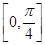 上的值域.
上的值域.