如图所示,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
(1)证明:DB=DC;
(2)设圆的半径为1,BC=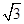 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.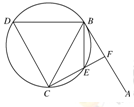
已知椭圆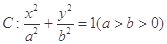 的离心率为
的离心率为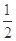 ,以原点O为圆心,椭圆的短半轴长为半径的圆与直线
,以原点O为圆心,椭圆的短半轴长为半径的圆与直线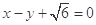 相切..
相切..
(1)求椭圆C的标准方程;
(2)若直线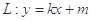 与椭圆C相交于A、B两点,且
与椭圆C相交于A、B两点,且 ,判断△AOB的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
,判断△AOB的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
已知函数 =
=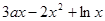 ,
,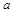 为常数.
为常数.
(1)当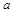 =1时,求
=1时,求 的单调区间;
的单调区间;
(2)若函数 在区间[1,2]上为单调函数,求
在区间[1,2]上为单调函数,求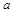 的取值范围.
的取值范围.
为了解某市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如下表:
(1)求本次评估的平均得分,并参照上表估计该市的总体交通状况等级;
(2)用简单随机抽样方法从这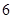 条道路中抽取
条道路中抽取 条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过
条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过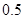 的概率.
的概率.
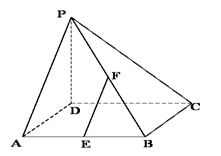
如图,在四棱锥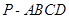 中,
中,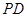 ⊥底面
⊥底面 ,底面
,底面 为正方形,
为正方形, ,
, ,
, 分别是
分别是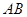 ,
,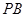 的中点.
的中点.
(1)求证: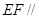 平面
平面 ;
;
(2)求证: ;
;
(3)设PD=AD= , 求三棱锥B-EFC的体积.
, 求三棱锥B-EFC的体积.