已知椭圆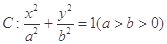 的离心率为
的离心率为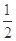 ,以原点O为圆心,椭圆的短半轴长为半径的圆与直线
,以原点O为圆心,椭圆的短半轴长为半径的圆与直线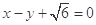 相切..
相切..
(1)求椭圆C的标准方程;
(2)若直线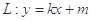 与椭圆C相交于A、B两点,且
与椭圆C相交于A、B两点,且 ,判断△AOB的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
,判断△AOB的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
(本小题满分12分)已知函数 ,其中a,b∈R,e=2.718 28 为自然对数的底数.
,其中a,b∈R,e=2.718 28 为自然对数的底数.
(1)设 是函数
是函数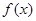 的导函数,求函数
的导函数,求函数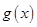 在区间
在区间 上的最小值;
上的最小值;
(2)若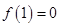 ,函数
,函数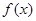 在区间(0,1)内有零点,求
在区间(0,1)内有零点,求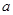 的取值范围.
的取值范围.
(本小题满分12分)已知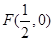 为抛物线
为抛物线 的焦点,点
的焦点,点
为其上一点,点M与点N关于x轴对称,直线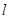 与抛物线交于异于M,N的A,B两点,且
与抛物线交于异于M,N的A,B两点,且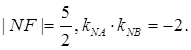
(1)求抛物线方程和N点坐标;
(2)判断直线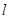 中,是否存在使得
中,是否存在使得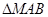 面积最小的直线
面积最小的直线 ,若存在,求出直线
,若存在,求出直线 的方程和
的方程和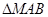 面积的最小值;若不存在,说明理由.
面积的最小值;若不存在,说明理由.
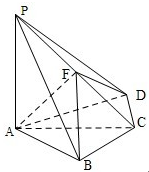
如图,四棱锥 中,
中, .
.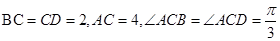 ,F为PC的中点,
,F为PC的中点,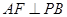 .
.
(1)求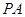 的长:
的长:
(2)求二面角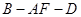 的正弦值.
的正弦值.
(本小题满分12分)在一个盒子中,放有大小相同的红、白、黄三个小球,现从中任意摸出一球,若是红球记1分,白球记2分,黄球记3分.现从这个盒子中,有放回地先后摸出两球,所得分数分别记为 、
、 ,设
,设 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,记
,记 .
.
(1)求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量 的分布列和数学期望.
的分布列和数学期望.
已知函数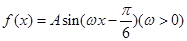 相邻两个对称轴之间的距离是
相邻两个对称轴之间的距离是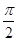 ,且满足,
,且满足,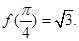
(1)求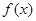 的单调递减区间;
的单调递减区间;
(2)在钝角△ABC中,a、b、c分别为角A、B、C的对边,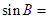
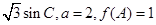 ,求△ABC的面积.
,求△ABC的面积.