某港口
要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口
北偏西30°且与该港口相距20海里的
处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过
小时与轮船相遇。
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由。
(本小题满分12分)在等差数列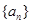 中,
中,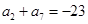 ,
,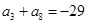 .
.
(1)求数列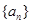 的通项公式;
的通项公式;
(2)设数列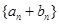 是首项为1,公比为
是首项为1,公比为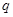 的等比数列,求
的等比数列,求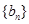 的前
的前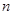 项和
项和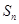 .
.
(本小题满分10分)选修4-5:不等式选讲
对于任意的实数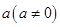 和
和 ,不等式
,不等式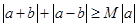 恒成立,记实数
恒成立,记实数 的最大值是
的最大值是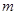 .
.
(1)求m的值;
(2)解不等式
(本小题满分10分)选修4-4:坐标系与参数方程
已知直线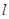 经过点
经过点 ,倾斜角
,倾斜角 ,圆C的极坐标方程为
,圆C的极坐标方程为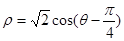
(1)写出直线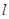 的参数方程,并把圆
的参数方程,并把圆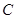 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)设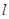 与圆
与圆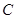 相交于两点
相交于两点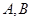 ,求点
,求点 到
到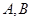 两点的距离之积.
两点的距离之积.
(本小题满分10分)选修4-1:几何证明选讲
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.
(1)求证: ;
;
(2)若 ,试求
,试求 的大小.
的大小.
(本小题满分12分)已知函数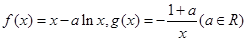 .
.
(1)当 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(2)设函数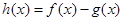 ,求函数
,求函数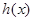 的单调区间;
的单调区间;
(3)若在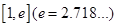 上存在一点
上存在一点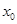 ,使得
,使得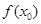 <
< 成立,求
成立,求 的取值范围.
的取值范围.