本题共有3个小题 ,第1小题满分4分,第2小题满分6分、第3小题满分6分.
,第1小题满分4分,第2小题满分6分、第3小题满分6分.
设 ,常数
,常数 ,定义运算“
,定义运算“ ”:
”: ,定义运算“
,定义运算“ ”:
”: ;对于两点
;对于两点 、
、 ,定义
,定义 .
.
(1)若 ,求动点
,求动点 的轨迹
的轨迹 ;
;
(2)已知直线 与(1)中轨迹
与(1)中轨迹 交于
交于 、
、 两点,若
两点,若 ,试求
,试求
 的值;
的值;
(3)在(2)中条件下,若直线 不过原点且与
不过原点且与 轴交于点S,与
轴交于点S,与 轴交于点T,并且与(1)中轨迹
轴交于点T,并且与(1)中轨迹 交于不同两点P、Q , 试求
交于不同两点P、Q , 试求 的取值范围.
的取值范围.
甲、乙两人连续6年对某县农村甲鱼养殖业的规模(产量)进行调查,提供了两个方面的信息如下图所示。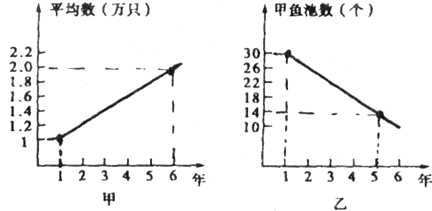
甲调查表明:每个甲鱼池平均出产量从第一年1万只甲鱼上升到第6年2万只。
乙调查表明:甲鱼池个数由第1年30个减少到第6年10个,请你根据提供的信息说明:
(1)第2年甲鱼池的个数及全县出产甲鱼总数;
(2)到第6年这个县的甲鱼养殖业的规模比第1年是扩大了还是缩小了?说明理由;
(3)哪一年的规模最大?说明理由
已知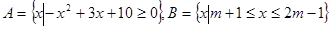 ,若
,若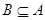 ,求实数
,求实数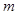 的取值范围.
的取值范围.
已知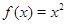 -
-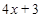 ,求
,求
(1)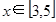 时,
时,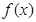 的最值。
的最值。
2. -1,
-1,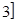 时,
时,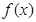 的最值。
的最值。
若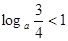
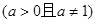 ,求实数
,求实数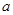 的取值范围。
的取值范围。
已知函数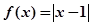 .
.
(1)用分段函数的形式表示该函数;
(2)在右边所给的坐标系中画出该函数的图象;
(3)写出该函数的定义域、值域、奇偶性、单调区间(不要求证明).