(本题满分14分,第(1)小题4分,第(2)小题4分,第(2)小题6分)
设数列 中,若
中,若 ,则称数列
,则称数列 为“凸数列”。
为“凸数列”。
(1)设数列 为“凸数列”,若
为“凸数列”,若 ,试写出该数列的前6项,并求出该6项之和;
,试写出该数列的前6项,并求出该6项之和;
(2)在“凸数列” 中,求证:
中,求证: ;
;
(3)设 ,若数列
,若数列 为“凸数列”,求数列前
为“凸数列”,求数列前 项和
项和 。
。
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度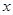 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过40辆/千米时,车流速度为80千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过40辆/千米时,车流速度为80千米/小时.研究表明:当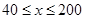 时,车流速度
时,车流速度 是车流密度
是车流密度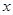 的一次函数.(1)当
的一次函数.(1)当 时,求函数
时,求函数 的表达式;
的表达式;
(2)当车流密度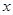 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位: 辆/小时)f
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位: 辆/小时)f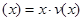 ,
,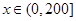 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
给出30个数:1,2,4,7,……,其规律是:第1个数是1,第2个数比第1个数大1, 第3个数比第2个数大2,第4个数比第3个数大3,依此类推.要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示)
(I)请在图中判断框内(1)处和执行框中的(2)处填上合适的语句,使之能完成该题算法功能;
(II)根据程序框图写出程序.
已知函数f(x)=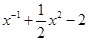 ,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1).
,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1).
已知 若
若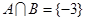 ,求实数
,求实数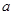 的值.
的值.
已知函数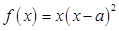 ,
,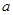 是大于零的常数.
是大于零的常数.
(Ⅰ)当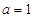 时,求
时,求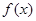 的极值;
的极值;
(Ⅱ)若函数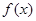 在区间
在区间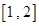 上为单调递增,求实数
上为单调递增,求实数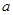 的取值范围;
的取值范围;
(Ⅲ)证明:曲线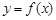 上存在一点
上存在一点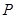 ,使得曲线
,使得曲线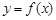 上总有两点
上总有两点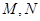 ,且
,且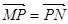 成立.
成立.