(本题满分14分,其中第1小题8分,第2小题6分)
一企业生产的某产品在不做电视广告的前提下,每天销售量为 件. 经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量
件. 经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量 (件)与电视广告每天的播放量
(件)与电视广告每天的播放量 (次)的关系可用如图所示的程序框图来体现.
(次)的关系可用如图所示的程序框图来体现.
(1)试写出该产品每天的销 售量
售量 (件)关于电视广告每天的播放量
(件)关于电视广告每天的播放量 (次)的函数关系式;
(次)的函数关系式;
(2)要使该产品每天的销售量比不做电视广告时的销售量至少增加 ,则每天电视广告的播放量至少需多少次?
,则每天电视广告的播放量至少需多少次?
设矩阵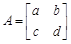 ,矩阵A属于特征值
,矩阵A属于特征值 的一个特征向量
的一个特征向量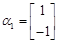 ,属于特征值
,属于特征值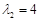 的一个特征向量
的一个特征向量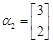 ,求
,求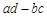 的值
的值
(本小题满分为16分)已知函数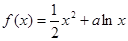 .
.
(1)若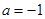 ,求函数
,求函数 的极值,并指出极大值还是极小值;
的极值,并指出极大值还是极小值;
(2)若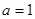 ,求函数
,求函数 在
在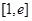 上的最值;
上的最值;
(3)若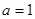 ,求证:在区间
,求证:在区间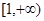 上,函数
上,函数 的图象在
的图象在 的图象下方.
的图象下方.
(本小题满分为16分)设A,B分别为椭圆
 的左、右顶点,椭圆的长轴长为
的左、右顶点,椭圆的长轴长为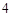 ,且点
,且点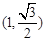 在该椭圆上.
在该椭圆上.
(1)求椭圆的方程;
(2)设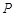 为直线
为直线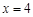 上不同于点
上不同于点 的任意一点,若直线
的任意一点,若直线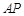 与椭圆相交于异于
与椭圆相交于异于 的点
的点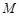 ,证明:△
,证明:△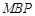 为钝角三角形.
为钝角三角形.
(本小题满分为16分)为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,新上了把二氧化碳处理转化为一种可利用的化工产品的项目,经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为: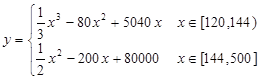 ,且每处理一吨二氧化碳得到可利用的化工产品价值为200元,若该项目不获利,国家将给予补偿.
,且每处理一吨二氧化碳得到可利用的化工产品价值为200元,若该项目不获利,国家将给予补偿.
(1)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则国家每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(本小题满分为14分)如图1所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的平分线,点E在线段AC上,CE=4.如图2所示,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连结AB,设点F是AB的中点.
(1)求证:DE⊥平面BCD;
(2)在图2中,若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥BDEG的体积.