威力实施“爱的教育”实践活动,宇华教育集团决定举行“爱在宇华”教师演讲比赛.焦作校区决定从高中部、初中部、小学部和幼教部这四个部门选出12人组成代表队代表焦作校区参赛,选手来源如下表:
| 部门 |
高中部 |
初中部 |
小学部 |
幼教部 |
| 人数 |
4 |
4 |
2 |
2 |
焦作校区选手经过出色表现获得冠军,现要从中选出两名选手代表冠军队发言.
(1)求这两名队员来自同一部门的概率;
(2)设选出的两名选手中来自高中部的人数为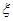 ,求随机变量
,求随机变量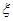 的分布列及数学期望
的分布列及数学期望 .
.
(本小题满分13分)已知函数 ,其中
,其中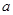 为常数,且
为常数,且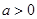 .
.
(1)若曲线 在点
在点 处的切线与直线
处的切线与直线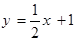 垂直,求
垂直,求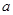 的值;
的值;
(2)若函数 在区间
在区间 上的最小值为
上的最小值为 ,求
,求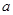 的值.
的值.
(本小题满分13分)如图所示的“8”字形曲线是由两个关于 轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是
轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是 ,双曲线的左、右顶点
,双曲线的左、右顶点 、
、 是该圆与
是该圆与 轴的交点,双曲线与半圆相交于与
轴的交点,双曲线与半圆相交于与 轴平行的直径的两端点.
轴平行的直径的两端点.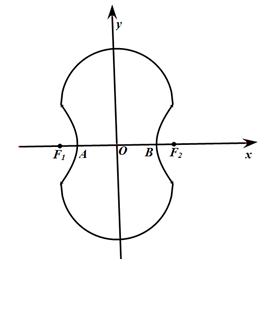
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为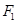 、
、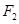 ,试在“8”字形曲线上求点
,试在“8”字形曲线上求点 ,使得
,使得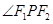 是直角.
是直角.
(本小题满分13分)设函数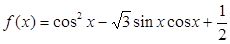
(Ⅰ)求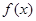 的最小正周期及值域;
的最小正周期及值域;
(Ⅱ)已知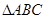 中,角
中,角 的对边分别为
的对边分别为 ,若
,若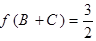 ,
, ,
,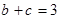 ,求
,求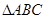 的面积.
的面积.
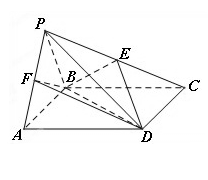
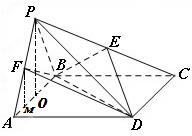
(本小题满分12分)如图,四棱锥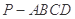 中,
中,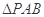 是正三角形,四边形
是正三角形,四边形 是矩形,且平面
是矩形,且平面
 平面
平面 ,
,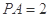 ,
,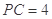 .
.
(Ⅰ)若点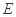 是
是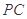 的中点,求证:
的中点,求证: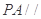 平面
平面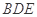 ;
;
(Ⅱ)若点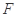 在线段
在线段 上,且
上,且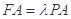 ,当三棱锥
,当三棱锥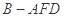 的体积为
的体积为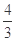 时,求实数
时,求实数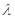 的值.
的值.
(本小题满分12分)
某网站针对“2015年春节放假安排”开展网上问卷调查,提出了A,B两种放假方案,调查结果如下表(单位:万人):
| 人群 |
青少年 |
中年人 |
老年人 |
| 支持A方案 |
200 |
400 |
800 |
| 支持B方案 |
100 |
100 |
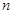 |
已知从所有参与调查的人中任选1人是“老年人”的概率为 .
.
(Ⅰ)求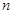 的值;
的值;
(Ⅱ)从参与调查的“老年人”中,用分层抽样的方法抽取6人,在这6人中任意选取2人,求恰好有1人“支持B方案”的概率.