(本小题满分12分)
某网站针对“2015年春节放假安排”开展网上问卷调查,提出了A,B两种放假方案,调查结果如下表(单位:万人):
| 人群 |
青少年 |
中年人 |
老年人 |
| 支持A方案 |
200 |
400 |
800 |
| 支持B方案 |
100 |
100 |
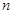 |
已知从所有参与调查的人中任选1人是“老年人”的概率为 .
.
(Ⅰ)求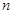 的值;
的值;
(Ⅱ)从参与调查的“老年人”中,用分层抽样的方法抽取6人,在这6人中任意选取2人,求恰好有1人“支持B方案”的概率.
(本小题满分14分)已知函数 (其中
(其中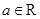 ,无理数
,无理数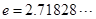 ).当
).当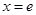 时,函数
时,函数 有极大值
有极大值 .
.
(1)求实数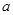 的值;
的值;
(2)求函数 的单调区间;
的单调区间;
(3)任取 ,
,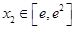 ,证明:
,证明: .
.
(本小题满分14分)平面内一动点 到定点
到定点 和到定直线
和到定直线 的距离相等,设
的距离相等,设 的轨迹是曲线
的轨迹是曲线 .
.
(1)求曲线 的方程;
的方程;
(2)在曲线 上找一点
上找一点 ,使得点
,使得点 到直线
到直线 的距离最短,求出
的距离最短,求出 点的坐标;
点的坐标;
(3)设直线
 ,问当实数
,问当实数 为何值时,直线
为何值时,直线 与曲线
与曲线 有交点?
有交点?
(本小题满分14分)北京市周边某工厂生产甲、乙两种产品.一天中,生产一吨甲产品、一吨乙产品所需要的煤、水以及产值如表所示:
| 用煤(吨) |
用水(吨) |
产值(万元) |
|
| 生产一吨甲种产品 |
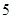 |
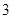 |
 |
| 生产一吨乙种产品 |
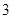 |
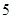 |
 |
在 会议期间,为了减少空气污染和废水排放.北京市对该厂每天用煤和用水有所限制,每天用煤最多
会议期间,为了减少空气污染和废水排放.北京市对该厂每天用煤和用水有所限制,每天用煤最多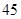 吨,用水最多
吨,用水最多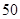 吨.问该厂如何安排生产,才能是日产值最大?最大的产值是多少?
吨.问该厂如何安排生产,才能是日产值最大?最大的产值是多少?
(本小题满分14分)已知等差数列 中,
中, ,
, ,各项为正数的等比数列
,各项为正数的等比数列 中,
中, ,
, .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)对于函数 ,若
,若 满足
满足 ,
, ,
, ,求
,求 及
及 的长.
的长.