(本小题满分12分)
已知:在△ABC中,a,b,c分别是角A、B、C所对的边,向量m=(2 sin
sin ,
, ),
),
n=(sin +
+ ,1)且m·n=
,1)且m·n= .
.
(1)求角B的大小;
(2)若角B为锐角,a=6,S△ABC=6 ,求b的值.
,求b的值.
已知二次函数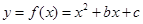 的图象过点(1,13),
的图象过点(1,13),
且函数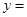
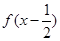 是偶函数.
是偶函数.
(1)求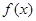 的解析式;
的解析式;
(2)已知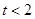 ,
,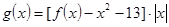 ,求函数
,求函数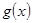 在[
在[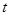 ,2]上的最大值和最小值.
,2]上的最大值和最小值.
已知函数 是奇函数,且
是奇函数,且 .
.
(1) 求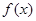 的表达式;(2) 设
的表达式;(2) 设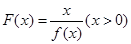 ;
;
记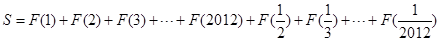 ,求S的值.
,求S的值.
已知函数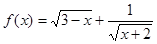 的定义域为集合
的定义域为集合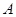 ,
,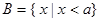 .
.
(1)若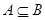 ,求实数a的取值范围;
,求实数a的取值范围;
(2)若全集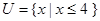 ,a=
,a=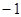 ,求
,求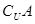 及
及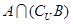 .
.
(本题12分)如图,在侧棱锥垂直底面的四棱锥ABCD-A1B1C1D1中,AD∥BC,
AD⊥AB,AB= 。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
与直线AA1的交点。
(1)证明:(i)EF∥A1D1;
(ii)BA1⊥平面B1C1EF;
(2)求BC1与平面B1C1EF所成的角的正弦值。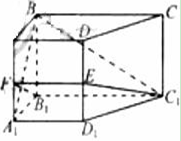
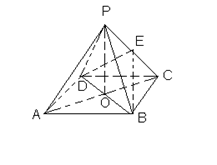
(本题8分)如图,ABCD是正方形,O是正方形的中心, PO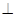 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。
求证:(1)PA∥平面BDE(2)平面PAC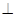 平面BDE
平面BDE