( 本小题满分12分)
本小题满分12分)
如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABC D.
(1)证明:BD⊥AA1;
(2)证明:平面AB1C//平面DA1C1 (3)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
(3)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
在直角坐标系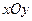 中,点P到两点
中,点P到两点 ,
, 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为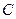 ,直线
,直线 与C交于A,B两点.
与C交于A,B两点.
(1)写出C的方程;
(2)若OA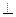 OB,求k的值
OB,求k的值
函数f(x)= 4x3+ax2+bx+5的图在x=1处的切线方程为y=-12x;
(1)求函数f(x)的解析式;
(2)求函数f(x)在 [—3,1]上的最值
在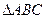 中,
中,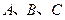 是三角形的三内角,
是三角形的三内角,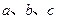 是三内角对应的三边,已知
是三内角对应的三边,已知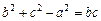 .
.
(Ⅰ)求角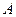 的大小;
的大小;
(Ⅱ)若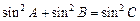 ,求角
,求角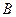 的大小
的大小
已知定义在区间[-p,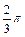 ]上的函数y=f(x)的图象关于直线x=-
]上的函数y=f(x)的图象关于直线x=-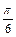 对称,当x
对称,当x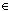 [-
[-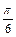 ,
,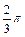 ]时,函数f(x)=Asin(wx+j)(A>0, w>0,-
]时,函数f(x)=Asin(wx+j)(A>0, w>0,-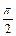 <j<
<j<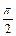 ),其图象如图所示。
),其图象如图所示。
(1)求函数y=f(x)在[-p,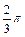 ]的表达式;
]的表达式;
(2)求方程f(x)=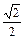 的解。
的解。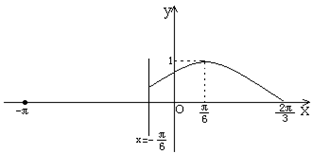
已知函数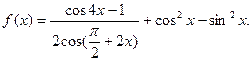
(Ⅰ)求函数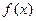 的定义域,值域。
的定义域,值域。
(Ⅱ)求函数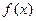 的最小正周期和单调递减区间
的最小正周期和单调递减区间