(本小题满分12分)
设O为坐标原点,点P的坐标
(I)在一个盒子中,放有标号为1,2,3的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为x,y,求|OP|的最
 大值,并求事件“|OP|取到最大值”的概率;
大值,并求事件“|OP|取到最大值”的概率;
(II)若利用计算机随机在[0,3]上先后取两个数分别记为x,y,求P点在第一象限的概率.
己知函数 的定义域为
的定义域为 , 函数
, 函数 的值域为
的值域为 ,不等式
,不等式 的解集为
的解集为
(1)求A
(2)若同时满足A,B的 值也满足C,求
值也满足C,求 的取值范围;
的取值范围;
(  13分)设函数
13分)设函数
(1)研究函数
 的单调性;
的单调性;
(2)判断 的实数解的个数,并加以证明.
的实数解的个数,并加以证明.
已知圆
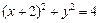 ,相互垂直的两条直线
,相互垂直的两条直线 、
、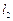 都过点
都过点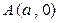 .
.
(Ⅰ)当 时,若圆心为
时,若圆心为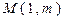 的圆和圆
的圆和圆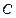 外切且与直线
外切且与直线 、
、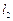 都相切,求圆
都相切,求圆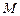 的方程;
的方程;
(Ⅱ)当 时,求
时,求 、
、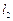 被圆
被圆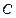 所截得
所截得 弦长之和的最大值.
弦长之和的最大值.
如图,当甲船位于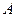 处时获悉,在其正东方向相距20海里的
处时获悉,在其正东方向相距20海里的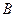 处有一艘渔船遇险
处有一艘渔船遇险 等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30
等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30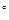 ,相距10海里
,相距10海里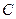 处的乙船.
处的乙船.
(Ⅰ)求处于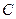 处的乙船和遇险渔船间的距离;
处的乙船和遇险渔船间的距离;
(Ⅱ)设乙船沿直线 方向前往
方向前往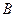 处救援,其方向与
处救援,其方向与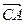 成
成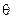 角,求
角,求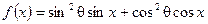
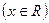 的值域.
的值域.
在公差为
 的等差数列
的等差数列 和公比为
和公比为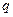 的等比数列
的等比数列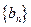 中,已知
中,已知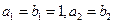 ,
,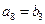 .
.
(Ⅰ)求数列 与
与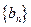 的通项公式;
的通项公式;
(Ⅱ)是否存在常数 ,使
,使 得对于一切正整数
得对于一切正整数 ,都有
,都有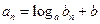 成立?若存在,求出常数
成立?若存在,求出常数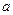 和
和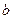 ,若不存在说明理由
,若不存在说明理由