有关专家建议,在未来几年内,中国的通货膨胀率保持在3%左右,这将对我国经济的稳定有利无害.所谓通货膨胀率为3%,指的是每年消费品的价格增长率为3%.在这种情况下,某种品牌的钢琴2004年的价格是10 000元,请用流程图描述这种钢琴今后四年的价格变化情况,并输出四年后的价格.
对于企业来说,生产成本、销售收入和利润之间的关系是个重要的问题.对一家药品生产企业的研究表明:该企业的生产成本 (单位:万元)和生产收入
(单位:万元)和生产收入 (单位:万元)都是产量
(单位:万元)都是产量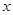 (单位:
(单位: )的函数,它们分别为
)的函数,它们分别为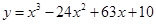 和
和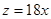 .
.
(1)试求出该企业获得的生产利润 (单位:万元)与产量
(单位:万元)与产量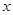 之间的函数关系式;
之间的函数关系式;
(2)当产量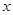 为多少时,该企业可获得最大利润?最大利润为多少?
为多少时,该企业可获得最大利润?最大利润为多少?
已知函数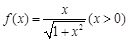 ,数列
,数列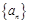 满足
满足 ,
, .
.
(1)求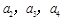 ;
;
(2)猜想数列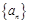 的通项,并用数学归纳法予以证明.
的通项,并用数学归纳法予以证明.
(1)若 的展开式中,
的展开式中,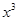 的系数是
的系数是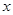 的系数的
的系数的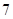 倍,求
倍,求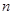 ;
;
(2)已知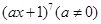 的展开式中,
的展开式中, 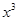 的系数是
的系数是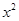 的系数与
的系数与 的系数的等差中项,求
的系数的等差中项,求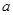 ;
;
(3)已知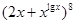 的展开式中,二项式系数最大的项的值等于
的展开式中,二项式系数最大的项的值等于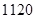 ,求
,求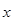 .
.
已知复数 ,当实数
,当实数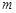 为何值时:
为何值时:
(1)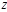 为实数;
为实数;
(2) 为虚数;
为虚数;
(3) 为纯虚数;
为纯虚数;
(4)复数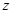 对应的点
对应的点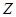 在第四象限.
在第四象限.
已知数列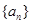 的相邻两项
的相邻两项 ,
, 是关于
是关于 方程
方程 的两根,且
的两根,且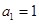 .
.
(1)求证:数列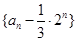 是等比数列;(2)求数列
是等比数列;(2)求数列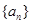 的前
的前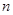 项和
项和 ;
;
(3)设函数 ,若
,若 对任意的
对任意的 都成立,求实数
都成立,求实数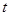 的范围.
的范围.