青年歌手电视大奖赛共有10名选手参加,并请了12名评委,在计算每位选手的平均分数时,为了避免个别评委所给的极端分数的影响,必须去掉一个最高分和一个最低分后再求平均分数,试设计一个算法,解决该问题,要求画出程序框图(假定分数采用10分制,即每位选手的分数最低为0分,最高为10分).
(本题满分 分) 某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
分) 某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
(I)假设n=2,求第一大块地都种植品种甲的概率;
(II)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如下表:
| 品种甲 |
403 |
397 |
390 |
404 |
388 |
400 |
412 |
406 |
| 品种乙 |
419 |
403 |
412 |
418 |
408 |
423 |
400 |
413 |
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
附:样本数据 的的样本方差
的的样本方差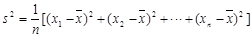 ,其中
,其中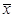 为样本平均数.
为样本平均数.
(本题满分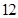 分)
分)
某超市一个月的收入和支出总共记录了N个数据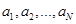 ,其中收入记为正数,支出记为负数。该超市用下面的程序框图计算月总收入S和月净盈利V,请将程序框图补充完整,将①②③处的内容填在下面对应的横线上。(要求:画出程序框并填写相应的内容)
,其中收入记为正数,支出记为负数。该超市用下面的程序框图计算月总收入S和月净盈利V,请将程序框图补充完整,将①②③处的内容填在下面对应的横线上。(要求:画出程序框并填写相应的内容)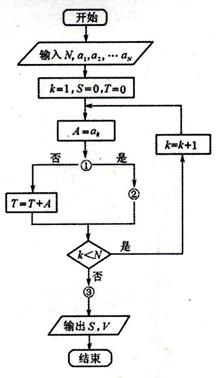
①处应填_____________________________。
②处应填_____________________________。
③处应填_____________________________。
(本题满分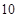 分)为了解高二学生的体能情况,某校抽取部分学生进行一分钟跳
分)为了解高二学生的体能情况,某校抽取部分学生进行一分钟跳
绳次数的测试,将所得数据整理、分组后,画出频率分布直方图(如图).图中从左到右各小长方形面积之比为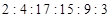 .若第二组的频数为
.若第二组的频数为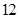 .
.
(1) 求第二组的频率是多少?样本容量是多少?
(2)若次数在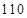 以上(含
以上(含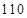 次)为达标,试估计该学校全体高二学生的达标率是多少?
次)为达标,试估计该学校全体高二学生的达标率是多少?
(本小题满分14分)
已知函数f(x)=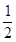 x
x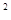 -ax + (a-1)
-ax + (a-1)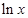 ,
,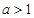 .
.
(I)讨论函数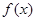 的单调性;
的单调性;
(II)若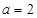 ,数列
,数列 满足
满足 .
.
(1)若首项 ,证明数列
,证明数列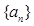 为递增数列;
为递增数列;
(2)若首项为正整数,数列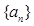 递增,求首项的最小值.
递增,求首项的最小值.
(本小题满分12分)
有甲、乙两种相互独立的预防措施可以降低某地区某灾情的发生.单独采用甲、乙预防措施后,灾情发生的概率分别为0.08和0.10,且各需要费用60万元和50万元.在不采取任何预防措施的情况下发生灾情的概率为0.3.如果灾情发生,将会造成800万元的损失.(设总费用=采取预防措施的费用+可能发生灾情损失费用)
(I)若预防方案允许甲、乙两种预防措施单独采用,他们各自总费用是多少?
(II)若预防方案允许甲、乙两种预防措施单独采用、联合采用或不采用,请确定预防方案使总费用最少的那个方案.