(本小题满分12分)在某高校自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为 五个等级.某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为
五个等级.某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为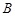 的考生有
的考生有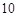 人.
人.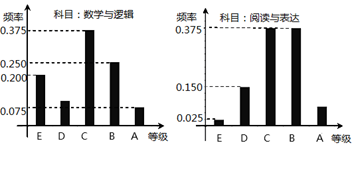
(Ⅰ)求该考场考生中“阅读与表达”科目中成 绩为 的人数;
的人数;
(Ⅱ)若等级 分别对应
分别对应 分,
分, 分,
分,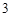 分,
分, 分,
分, 分,求该考场考生“数学与逻辑”科目的平均分;
分,求该考场考生“数学与逻辑”科目的平均分;
(Ⅲ)已知参加本考场测试的考生中,恰有两人的两科成绩均为 .在至少一科成绩为
.在至少一科成绩为 的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为
的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为 的概率.
的概率.
(本小题满分10分)选修4-1:几何证明选讲
已知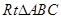 (
(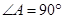 )的外接圆为圆
)的外接圆为圆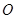 ,过
,过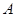 的切线
的切线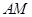 交
交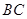 于点
于点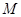 ,过
,过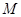 作直线交
作直线交 于点
于点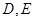 ,且
,且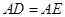
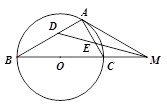
(1)求证: 平分角
平分角 ;
;
(2)已知 ,求
,求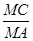 的值.
的值.
(本小题满分12分)已知函数 为常数)的所有极值之和为零;
为常数)的所有极值之和为零;
(1)求 及
及 的极大值点;
的极大值点;
(2)若 的极大值为
的极大值为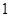 ,对任意
,对任意 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知椭圆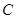 :
: ,其通径(过焦点且与x轴垂直的直线被椭圆截得的线段)长
,其通径(过焦点且与x轴垂直的直线被椭圆截得的线段)长 .
.
(1)求椭圆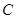 的方程;
的方程;
(2)设过椭圆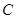 右焦点的直线(不与
右焦点的直线(不与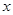 轴重合)与椭圆交于
轴重合)与椭圆交于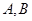 两点,问在
两点,问在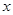 轴上是否存在一点
轴上是否存在一点 ,使
,使 为常数?若存在,求点
为常数?若存在,求点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
本小题满分12分)在平行六面体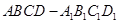 中,
中, ,
,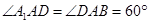 ,
,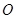 是
是 的中点.
的中点.
(1)证明: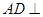 面
面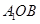 ;
;
(2)若 ,求直线
,求直线 与平面
与平面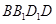 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)某电视台有一档综艺节目,其中有一个抢答环节,有甲、乙两位选手进行抢答,规则如下:若选手抢到答题权,答对得20分,答错或不答则送给对手10分.已知甲每次抢到答题权的概率为 ,且答对的概率为
,且答对的概率为 ,乙抢到答题权的概率为
,乙抢到答题权的概率为 ,且答对的概率为
,且答对的概率为 .
.
(1)在一轮抢答中,甲得到0分的概率;
(2)若比赛进行两轮,求甲得分的分布列及其期望.