(本小题满分12分)某电视台有一档综艺节目,其中有一个抢答环节,有甲、乙两位选手进行抢答,规则如下:若选手抢到答题权,答对得20分,答错或不答则送给对手10分.已知甲每次抢到答题权的概率为 ,且答对的概率为
,且答对的概率为 ,乙抢到答题权的概率为
,乙抢到答题权的概率为 ,且答对的概率为
,且答对的概率为 .
.
(1)在一轮抢答中,甲得到0分的概率;
(2)若比赛进行两轮,求甲得分的分布列及其期望.
设曲线 处的切线l与x轴、y轴所围成的三角形面积为S(t).
处的切线l与x轴、y轴所围成的三角形面积为S(t).
(Ⅰ)求切线l的方程;
(Ⅱ)求S(t)的最大值.
已知函数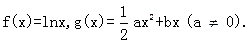
(I)若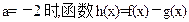 在其定义域是增函数,求b的取值范围;
在其定义域是增函数,求b的取值范围;
(II)在(I)的结论下,设函数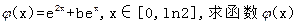 的最小值;
的最小值;
(III)设函数 的图象C1与函数
的图象C1与函数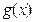 的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
已知函数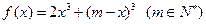 .
.
(Ⅰ)若 、
、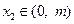 ,求证:①
,求证:① ;
;
② .
.
(Ⅱ)若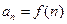 ,
,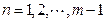 ,其中
,其中 ,求证:
,求证: ;
;
(Ⅲ)对于任意的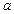 、
、 、
、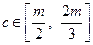 ,问:以
,问:以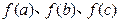 的值为长的三条线段是否可构成三角形?请说明理由.
的值为长的三条线段是否可构成三角形?请说明理由.
已知二次函数 的二次项系数为
的二次项系数为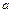 ,且不等式
,且不等式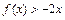 的解集为
的解集为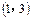

⑴若方程 有两个相等的实数根,求
有两个相等的实数根,求 的解析式;
的解析式;
⑵若函数 无极值,求实数
无极值,求实数 的取值范围
的取值范围
设函数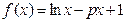
(1)求函数 的极值点
的极值点
(2)当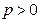 时,若对任意的
时,若对任意的 ,恒有
,恒有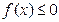 ,求
,求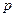 的取值范围
的取值范围
(3)证明: