设曲线 处的切线l与x轴、y轴所围成的三角形面积为S(t).
处的切线l与x轴、y轴所围成的三角形面积为S(t).
(Ⅰ)求切线l的方程;
(Ⅱ)求S(t)的最大值.
已知四棱锥P-ABCD的正视图是一个底边长为4,腰长为3的等腰三角形,如图分别是四棱锥P-ABCD的侧视图和俯视图.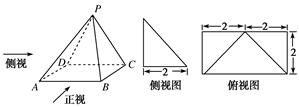
(1)求证:AD⊥PC;
(2)求四棱锥P-ABCD的侧面PAB的面积.
设角A,B,C为△ABC的三个内角.
(1)设f(A)=sin A+2sin 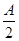 ,当A取A0时,f(A)取极大值f(A0),试求A0和f(A0)的值;
,当A取A0时,f(A)取极大值f(A0),试求A0和f(A0)的值;
(2)当A取A0时,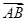 ·
·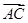 =-1,求BC边长的最小值.
=-1,求BC边长的最小值.
如图,在几何体ABCDE中,AB=AD=2,AB⊥AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,且AE=MC=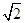 .
.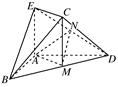
(1)求证:平面BCD⊥平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC.
已知m=(2cos x+2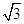 sin x,1),n=(cos x,-y),且m⊥n.
sin x,1),n=(cos x,-y),且m⊥n.
(1)将y表示为x的函数f(x),并求f(x)的单调递增区间;
(2)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f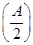 =3,且a=2,b+c=4,求△ABC的面积.
=3,且a=2,b+c=4,求△ABC的面积.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.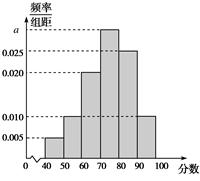
(1)求图中实数a的值;
(2)若该校高一年级共有学生640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.