打鼾不仅影响别人休息,而且可能与患某种疾病有关,下表是一次调查所得的数据,试问:第一晚都打鼾与患心脏病有关吗?试用图形和独立性检验的方法进行判断。
| 患心脏病 |
未患心脏病 |
合计 |
|
| 每一晚都打鼾 |
30 |
224 |
254 |
| 不打鼾 |
24 |
1355 |
1379 |
| 合计 |
54 |
1579 |
1633 |
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“ ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
在一次恶劣气候的飞机航程中,调查了男女乘客在飞机上晕机的情况:男乘客晕机的有24人,不晕机的有31人;女乘客晕机的有8人,不晕机的有26人。请你根据所给数据判定是否在恶劣气候飞行中男人比女人更容易晕机?
解:因为函数没有零点,所以方程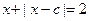 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
某地区的羊患某种病的概率是0.4,且每只羊患病与否是彼此独立的,今研制一种新的预防药,任选6只羊做实验,结果6只羊服用此药后均未患病. 你认为这种药是否有效?
在讲述 与
与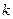 的关系时,有的同学认为
的关系时,有的同学认为 与
与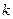 的是一样的,无非
的是一样的,无非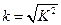 而已,你认为这种说法正确吗?为什么?
而已,你认为这种说法正确吗?为什么?
为了研究患慢性气管炎与吸烟量的关系,调查了228人,其中每天的吸烟支数在10支以上的20支以下的调查者中,患者人数有98人,非患者人数有89人,每天的吸烟支数在20支以上的调查者中,患者人数有25人,非患者人数有16人。
(1)根据以上数据建立一个2×2的列联表;
(2),试问患慢性气管炎是否与吸烟量相互独立?
参考公式:
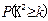 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
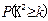 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |