已知函数 ,
,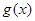 =
= 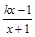 (
(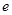 是自然对数的底)
是自然对数的底)
(1)若函数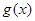 是(1,+∞)上的增函数,求
是(1,+∞)上的增函数,求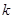 的取值范围;
的取值范围;
(2)若对任意的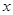 >0,都有
>0,都有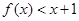 ,求满足条件的最大整数
,求满足条件的最大整数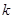 的值;
的值;
(3)证明: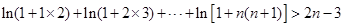 ,
, .
.
设函数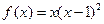 ,
,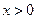 .
.
⑴求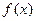 的极值;
的极值;
⑵设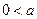 ≤
≤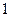 ,记
,记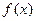 在
在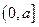 上的最大值为
上的最大值为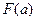 ,求函数
,求函数 的最小值;
的最小值;
⑶设函数 (
(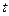 为常数),若使
为常数),若使 ≤
≤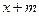 ≤
≤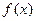 在
在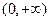 上恒成立的实数
上恒成立的实数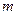 有且只有一个,求实数
有且只有一个,求实数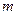 和
和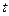 的值.
的值.
已知椭圆 :
: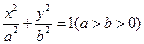 的离心率为
的离心率为 ,且过点
,且过点 ,设椭圆的右准线
,设椭圆的右准线 与
与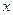 轴的交点为
轴的交点为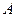 ,椭圆的上顶点为
,椭圆的上顶点为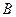 ,直线
,直线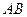 被以原点为圆心的圆
被以原点为圆心的圆 所截得的弦长为
所截得的弦长为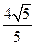 .
.
⑴求椭圆 的方程及圆
的方程及圆 的方程;
的方程;
⑵若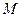 是准线
是准线 上纵坐标为
上纵坐标为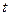 的点,求证:存在一个异于
的点,求证:存在一个异于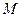 的点
的点 ,对于圆
,对于圆 上任意一点
上任意一点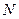 ,有
,有 为定值;且当
为定值;且当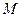 在直线
在直线 上运动时,点
上运动时,点 在一个定圆上.
在一个定圆上.
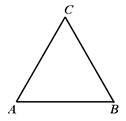
如图,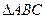 为一个等腰三角形形状的空地,腰
为一个等腰三角形形状的空地,腰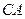 的长为
的长为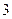 (百米),底
(百米),底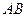 的长为
的长为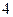 (百米).现决定在空地内筑一条笔直的小路
(百米).现决定在空地内筑一条笔直的小路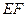 (宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为
(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为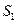 和
和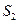 .
.
⑴若小路一端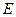 为
为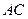 的中点,求此时小路的长度;
的中点,求此时小路的长度;
⑵求 的最小值.
的最小值.
在菱形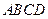 中,
中, ,线段
,线段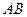 的中点是
的中点是 ,现将
,现将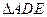 沿
沿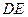 折起到
折起到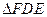 的位置,使平面
的位置,使平面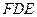 和平面
和平面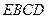 垂直,线段
垂直,线段 的中点是
的中点是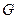 .
.
⑴证明:直线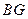 ∥平面
∥平面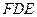 ;
;
⑵判断平面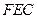 和平面
和平面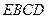 是否垂直,并证明你的结论.
是否垂直,并证明你的结论.
(本小题满分14分)
已知函数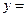
 的定义域为R, 且对于任意
的定义域为R, 且对于任意 R,存在正实数
R,存在正实数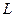 ,使得
,使得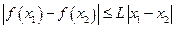 都成立.
都成立.
若 ,求
,求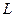 的取值范围;
的取值范围;
当 时,数列
时,数列 满足
满足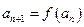 ,
, .
.
证明: ;
;
令 ,证明:
,证明: .
.