某单位要建造一个长方体无盖贮水箱,其容积为48m3,深为3m,如果池底每1m2的造价为40元,池壁每1m2的造价为20元,问怎样设计水箱能使总造价最低,最低总造价是多少元?
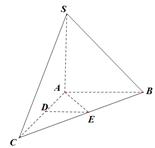
如图,在三棱锥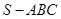 中,
中,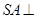 底面
底面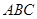 ,
,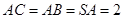 ,
,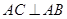 ,
,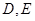 分别是
分别是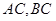 的中点,
的中点,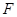 在
在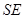 上,且
上,且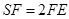 .
.
(1)求证: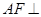 平面
平面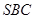 ;
;
(2)在线段上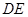 上是否存在点
上是否存在点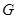 ,使二面角
,使二面角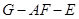 的大小为
的大小为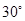 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
| 态度 调查人群 |
应该取消 |
应该保留 |
无所谓 |
| 在校学生 |
2100人 |
120人 |
 人 人 |
| 社会人士 |
600人 |
 人 人 |
 人 人 |
(1)已知在全体样本中随机抽取 人,抽到持“应该保留”态度的人的概率为
人,抽到持“应该保留”态度的人的概率为 ,现用分层抽样的方法在所有参与调查的人中抽取
,现用分层抽样的方法在所有参与调查的人中抽取 人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取 人,再平均分成两组进行深入交流,求第一组中在校学生人数
人,再平均分成两组进行深入交流,求第一组中在校学生人数 的分布列和数学期望.
的分布列和数学期望.
【改编题】已知向量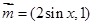 ,
,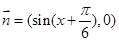 ,,函数
,,函数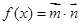 ,
,
(1)求函数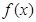 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)当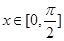 时,求函数
时,求函数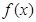 的值域.
的值域.
选修4—5:不等式选讲
已知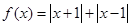 ,不等式
,不等式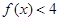 的解集为
的解集为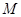 .
.
(1)求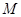 ;
;
(2)当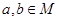 时,证明:
时,证明: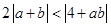 .
.
选修4—4:坐标系与参数方程
已知椭圆C: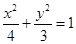 ,直线
,直线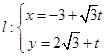 (t为参数).
(t为参数).
(Ⅰ)写出椭圆C的参数方程及直线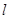 的普通方程;
的普通方程;
(Ⅱ)设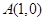 ,若椭圆C上的点P满足到点A的距离与其到直线
,若椭圆C上的点P满足到点A的距离与其到直线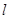 的距离相等,求点P的坐标.
的距离相等,求点P的坐标.