如图，半径为30
的圆形（
为圆心）铁皮上截取一块矩形材料
，其中点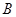
在圆弧上，点
在两半径上，现将此矩形材料卷成一个以
为母线的圆柱形罐子的侧面（不计剪裁和拼接损耗），设
与矩形材料的边
的夹角为
，圆柱的体积为
.
（Ⅰ）求关于的函数关系式？
（Ⅱ）求圆柱形罐子体积的最大值.
在数列{an}中，a1＝1，{an}的前n项和Sn满足2Sn＝an＋1.
(1)求数列{an}的通项公式；
(2)若存在n∈N*，使得λ≤
，求实数λ的最大值．
已知{an}为等差数列，且a2＝－1，a5＝8.
(1)求数列{|an|}的前n项和；
(2)求数列{2n·an}的前n项和．
已知数列{an}的前n项和Sn满足Sn＋an＋
n－1＝2(n∈N*)，设cn＝2nan.
(1)求证：数列{cn}是等差数列，并求数列{an}的通项公式．
(2)按以下规律构造数列{bn}，具体方法如下：
b1＝c1，b2＝c2＋c3，b3＝c4＋c5＋c6＋c7，…，第n项bn由相应的{cn}中2n－1项的和组成，求数列{bn}的通项bn.
已知n∈N*，数列{dn}满足dn＝
，数列{an}满足an＝d1＋d2＋d3＋…＋d2n，又知在数列{bn}中，b1＝2，且对任意正整数m，n，
.
(1)求数列{an}和数列{bn}的通项公式；
(2)将数列{bn}中的第a1项，第a2项，第a3项，…，第an项，…删去后，剩余的项按从小到大的顺序排成新数列{cn}，求数列{cn}的前2 013项和．
已知各项均不相等的等差数列{an}的前5项和为S5＝35，且a1＋1，a3＋1，a7＋1成等比数列．
(1)求数列{an}的通项公式；
(2)设Tn为数列
的前n项和，问是否存在常数m，使Tn＝m
，若存在，求m的值；若不存在，说明理由．