已知各项均不相等的等差数列{an}的前5项和为S5=35,且a1+1,a3+1,a7+1成等比数列.
(1)求数列{an}的通项公式;
(2)设Tn为数列 的前n项和,问是否存在常数m,使Tn=m
的前n项和,问是否存在常数m,使Tn=m ,若存在,求m的值;若不存在,说明理由.
,若存在,求m的值;若不存在,说明理由.
将一颗正方体的骰子先后抛掷2次(每个面朝上等可能),记下向上的点数,求:
(1)求两点数之和为5的概率;
(2)以第一次向上点数为横坐标 ,第二次向上的点数为纵坐标
,第二次向上的点数为纵坐标 的点
的点 在圆
在圆 的内部的概率.
的内部的概率.
已知函数 .(
.( 为常数)
为常数)
(1)当 时,①求
时,①求 的单调增区间;②试比较
的单调增区间;②试比较 与
与 的大小;
的大小;
(2) ,若对任意给定的
,若对任意给定的 ,在
,在 上总存在两个不同的
上总存在两个不同的 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
已知椭圆 的右焦点为
的右焦点为 ,离心率
,离心率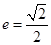 ,
,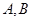 是椭圆上的两动点,动点
是椭圆上的两动点,动点 满足
满足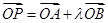 (其中实数
(其中实数 为常数).
为常数).
(1)求椭圆标准方程;
(2)当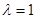 ,且直线
,且直线 过
过 点且垂直于
点且垂直于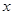 轴时,求过
轴时,求过 三点的外接圆方程;
三点的外接圆方程;
(3)若直线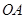 与
与 的斜率乘积
的斜率乘积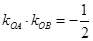 ,问是否存在常数
,问是否存在常数 ,使得动点
,使得动点 满足
满足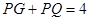 ,其中
,其中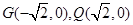 ,若存在求出
,若存在求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.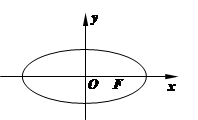
某商场销售某种商品的经验表明,该商品每日的销售量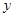 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式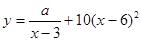 ,其中
,其中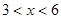 ,
,  为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求 的值;
的值;
(2)若该商品的成本为3元/千克, 试确定销售价格 的值,使商场每日销售该商品所获得的利润最大.
的值,使商场每日销售该商品所获得的利润最大.
设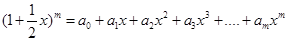 ,若
,若 成等差数列.
成等差数列.
(1) 求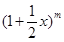 展开式的中间项;
展开式的中间项;
(2)求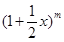 展开式中所有含
展开式中所有含 奇次幂的系数和.
奇次幂的系数和.