一个口袋中装有大小相同的2个红球,3个黑球和4个白球,从口袋中一次摸出一个球,摸出的球不再放回.
（Ⅰ）连续摸球2次,求第一次摸出黑球,第二次摸出白球的概率；
（Ⅱ）如果摸出红球,则停止摸球,求摸球次数不超过3次的概率．
如图，在锥体PABCD中，ABCD是边长为1的菱形，且∠DAB＝60°，PA＝PD＝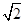
，PB＝2，E、F分别是BC、PC的中点．证明：AD⊥平面DEF.
由平面α外一点P引平面的三条相等的斜线段，斜足分别为A、B、C，O为△ABC的外心，求证：OP⊥α.
在正方体ABCD-A1B1C1D1中，E、F分别是CD、A1D1中点．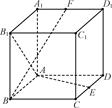
(1)求证：AB1⊥BF；
(2)求证：AE⊥BF；
(3)棱CC1上是否存在点F，使BF⊥平面AEP，若存在，确定点P的位置；若不存在，说明理由．
在正三棱柱ABCA1B1C1中，点D是BC的中点，BC＝BB1.
(1)若P是CC1上任一点，求证：AP不可能与平面BCC1B1垂直；
(2)试在棱CC1上找一点M，使MB⊥AB1.
在三棱锥SABC中，SA⊥平面ABC，SA＝AB＝AC＝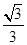
BC，点D是BC边的中点，点E是线段AD上一点，且AE＝3DE，点M是线段SD上一点，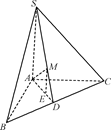
(1)求证：BC⊥AM；
(2)若AM⊥平面SBC，求证：EM∥平面ABS.