(本小题满分16分)已知椭圆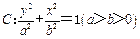 的离心率为
的离心率为 ,过右顶点A的直线l与椭圆C相交于A、B两点,且
,过右顶点A的直线l与椭圆C相交于A、B两点,且 .
.
(1)求椭圆C和直线l的方程;
(2)记曲线C在直线l下方的部分与线段AB所围成的平面区域(含边界)为D.若曲线 与D有公共点,试求实数m的最小值.
与D有公共点,试求实数m的最小值.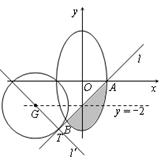
已知曲线 上任意一点
上任意一点 到两个定点
到两个定点 ,
, 的距离之和为4.
的距离之和为4.
(1)求曲线 的方程;
的方程;
(2)设过(0,-2)的直线 与曲线
与曲线 交于
交于 两点,且
两点,且 (
( 为原点),求直线
为原点),求直线 的方程.
的方程.
已知 ,且
,且 。
。
求证: 中至少有一个是负数。
中至少有一个是负数。
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与休闲方式是否有关系。
附:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
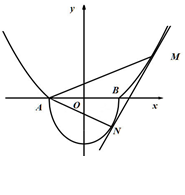
如图所示的曲线 是由部分抛物线
是由部分抛物线 和曲线
和曲线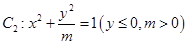 “合成”的,直线
“合成”的,直线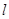 与曲线
与曲线 相切于点
相切于点 ,与曲线
,与曲线 相切于点
相切于点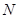 ,记点
,记点 的横坐标为
的横坐标为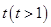 ,其中
,其中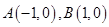 .
.
(1)当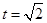 时,求
时,求 的值和点
的值和点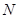 的坐标;
的坐标;
(2)当实数 取何值时,
取何值时, ?并求出此时直线
?并求出此时直线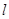 的方程.
的方程.
设抛物线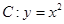 ,
,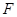 为焦点,
为焦点, 为准线,准线与
为准线,准线与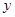 轴交点为
轴交点为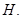
(1)求 ;
;
(2)过点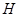 的直线与抛物线
的直线与抛物线 交于
交于 两点,直线
两点,直线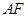 与抛物线交于点
与抛物线交于点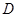 .
.
①设 三点的横坐标分别为
三点的横坐标分别为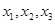 ,计算:
,计算: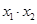 及
及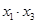 的值;
的值;
②若直线 与抛物线交于点
与抛物线交于点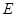 ,求证:
,求证: 三点共线.
三点共线.