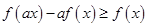
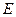
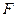
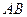
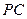
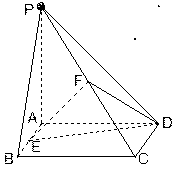
(1)求证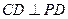 ;
;
(2)求证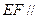 平面
平面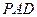 。
。
已知命题p:“任意的x∈[1,2],x2-a≥0”;
命题q:“存在x0∈R,x02+2ax0+2-a=0”,若命题“p且q”是真命题.
求实数a的取值范围.
已知函数 ,函数g(x)的导函数
,函数g(x)的导函数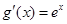 ,且
,且
(1)求 的极值;
的极值;
(2)若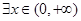 ,使得
,使得 成立,试求实数m的取值范围:
成立,试求实数m的取值范围:
(3)当a=0时,对于 ,求证:
,求证: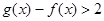
已知椭圆 点
点 ,离心率为
,离心率为 ,左右焦点分别为
,左右焦点分别为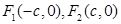
(1)求椭圆的方程;
(2)若直线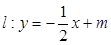 与椭圆交于
与椭圆交于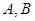 两点,与以
两点,与以 为直径的圆交于
为直径的圆交于 两点,且满足
两点,且满足 ,求直线
,求直线 的方程.
的方程.
如图2,四边形 为矩形,
为矩形,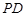 ⊥平面
⊥平面 ,
, ,作如图3折叠,折痕
,作如图3折叠,折痕

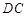 ,其中点
,其中点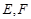 分别在线段
分别在线段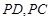 上,沿
上,沿 折叠后点
折叠后点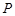 叠在线段
叠在线段 上的点记为
上的点记为 ,并且
,并且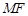 ⊥
⊥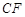 .(1)证明:
.(1)证明: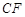 ⊥平面
⊥平面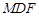 ;
;
(2)求三棱锥 的体积.
的体积.
已知函数 .
.
(1)解不等式 ;
;
(2)若 ,求证:
,求证: