
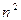
已知 =(cos2
=(cos2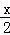 ,
,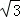 sinx),
sinx), =(2,1),设函数f(x)=
=(2,1),设函数f(x)=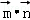 .
.
(1)当x ,求函数f(x)的值域;
,求函数f(x)的值域;
(2)当f(α)=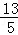 ,且﹣
,且﹣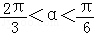 ,求sin(2
,求sin(2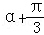 )的值.
)的值.
公差不为零的等差数列{an}中,a1、a2、a5成等比数列,且该数列的前10项和为100.
(1)求数列{an}的通项公式;
(2)若bn=an﹣10,求数列{bn}的前n项和Tn的最小值.
已知λ,μ为常数,且为正整数,λ≠1,无穷数列{an}的各项均为正整数,其前n项和为Sn,对任意的正整数n,Sn=λan﹣μ.记数列{an}中任意两不同项的和构成的集合为A.
(1)证明:无穷数列{an}为等比数列,并求λ的值;
(2)若2015∈A,求μ的值;
(3)对任意的n∈N*,记集合Bn={x|3μ•2n﹣1<x<3μ•2n,x∈A}中元素的个数为bn,求数列{bn}的通项公式.
已知函数f(x)=a(x+ )﹣|x﹣
)﹣|x﹣ |(x>0)a∈R.
|(x>0)a∈R.
(1)若a= ,求y=f(x)的单调区间;
,求y=f(x)的单调区间;
(2)若关于x的方程f(x)=t有四个不同的解x1,x2,x3,x4,求实数a,t应满足的条件;
(3)在(2)条件下,若x1,x2,x3,x4成等比数列,求t用a表示.
某工厂因排污比较严重,决定着手整治,一个月时污染度为60,整治后前四个月的污染度如表:
| 月数 |
1 |
2 |
3 |
4 |
… |
| 污染度 |
60 |
31 |
13 |
0 |
… |
污染度为0后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:f(x)=20|x﹣4|(x≥1), ,
, ,其中x表示月数,f(x)、g(x)、h(x)分别表示污染度.
,其中x表示月数,f(x)、g(x)、h(x)分别表示污染度.
(1)问选用哪个函数模拟比较合理?并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过60?