（本题满分16分；第（1）小题5分，第（2）小题5分，第（3）小题6分）
设
、
为坐标平面
上的点，直线
（
为坐标原点）与抛物线
交于点
(异于).
（1） 若对任意
，点在抛物线
上，试问当
为何值时，点
在某一圆上，并求出该圆方程
；
（2） 若点
在椭圆
上，试问：点能否在某一双曲线上，若能，求出该双曲线方程，若不能，说明理由；
（3） 对（1）中点所在圆方程，设
、
是圆上两点，且满足
，试问：是否存在一个定圆
，使直线
恒与圆相切.
12分）已知函数
（1）设
是正数组成的数列，前
项和为
，其中
，若点
在函数
的图象上，求证：点
也在的图象上；
（2）求函数
在区间
内的极值. 下
2分）已知
的展开式中，前三项的二项式系数之和为37.
（1）求x的整数次幂的项；
（2）展开式的第几项的二项式系数大于相邻两项的二项式系数.
在每道单项选择题给出的4个备选答案中，只有一个是正确的.若对4道选择题中的每一道都任意选定一个答案，求这4道题中：
（1）恰有两道题答对的概率；
（2）至少答对一道题的概率。
7名师生站成一排照相留念，其中老师1人，男生4人，女生2人，在下列情况下，各有不同站法多少种？
（1）两中女生必须相邻而站；
（2）4名男生互不相邻；
（3）若4名男生身高都不等，按从高到低的一种顺序站；
（4）老师不站中间，女生不站两端.
在△ABC中，a、b、c分别为角A、B、C的对边，已知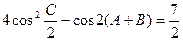
，c=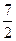
，又△ABC的面积为S△ABC=
，求a，b的值.