学校在开展学雷锋活动中,从高二甲乙两班各选3名学生参加书画比赛,其中高二甲班选出了1女2男,高二乙班选出了1男2女。
(1)若从6个同学中抽出2人作活动发言,写出所有可能的结果,并求高二甲班女同学,高二乙班男同学至少有一个被选中的概率。
(2)若从高二甲班和高二乙班各选一名现场作画,写出所有可能的结果,并求选出的2名同学性别相同的概率。
(本小题满分14分)如图所示,在棱长为2的正方体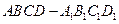 中,
中, 、
、 分
分
别为 、
、 的中点.
的中点.
(Ⅰ)求证: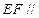 平面
平面 ;
;
(Ⅱ)求证: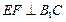 ;
;
(III)求三棱锥 的体积.
的体积.
(本小题满分13分)
已知椭圆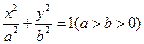 的左焦点为
的左焦点为 ,左右顶点分别为
,左右顶点分别为 ,上顶点为
,上顶点为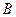 ,过
,过 三点作圆
三点作圆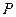 ,其中圆心
,其中圆心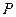 的坐标为
的坐标为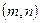 .
.
(Ⅰ)当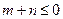 时,椭圆的离心率的取值范围.
时,椭圆的离心率的取值范围.
(Ⅱ)直线 能否和圆
能否和圆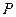 相切?证明你的结论.
相切?证明你的结论.
(本小题满分12分)
同时掷两个骰子,计算:
(Ⅰ)一共有多少种不同的结果?
(Ⅱ)其中向上的点数之和是5的结果有多少种?概率是多少?
(III)向上的点数之和小于5的概率是多少?
(本小题满分13分)
已知在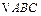 中,
中,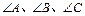 所对的边分别为
所对的边分别为 ,若
,若 且
且
(Ⅰ)求角A、B、C的大小;
(Ⅱ)设函数 ,求函数
,求函数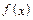 的单调递增区间,并指出它相邻两对称轴间的距离.
的单调递增区间,并指出它相邻两对称轴间的距离.
(本小题满分14分)设圆 ,将曲线上每一点的纵坐标压缩到原来的
,将曲线上每一点的纵坐标压缩到原来的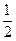 ,对应的横坐标不变,得到曲线C.经过点M(2,1),平行于OM的直线
,对应的横坐标不变,得到曲线C.经过点M(2,1),平行于OM的直线 在y轴上的截距为m(m≠0),
在y轴上的截距为m(m≠0), 交曲线C于A、B两个不同点.
交曲线C于A、B两个不同点.
(1)求曲线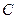 的方程;
的方程;
(2)求m的取值范围;
(3)求证直线MA、MB与x轴始终围成一个等腰三角形.