如图所示，足够长的水平导体框架的宽度L=0.5m，电阻忽略不计，定值电阻R=2Ω。磁感应强度B=0.8T的匀强磁场垂直于导体框平面，一根质量为m=0.2kg、有效电阻r=2Ω的导体棒MN垂直跨放在框架上，该导体棒与框架的动摩擦因数μ=0.5，导体棒在水平恒力F=1.2N的作用下由静止开始沿框架运动到刚好达到最大速度时，通过导体棒截面的电量共为q=2C，求：
（1）导体棒的最大速度；
（2）导体棒从开始运动到刚好达到最大速度这一过程中，导体棒运动的距离和导体棒产生的电热。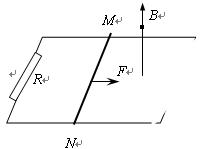
如图所示,一交流发电机的线圈在匀强磁场中匀速转动，线圈匝数N=100，线圈电阻r="3" Ω，ab="cd=0.5" m，bc="ad=0.4" m，磁感应强度B="0.5" T，电阻R="311" Ω，当线圈以n="300" r/min的转速匀速转动时，求: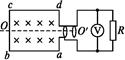
(1)感应电动势的最大值；
(2)t=0时线圈在图示位置，写出此交变电流电动势瞬时值表达式；
(3)此电压表的示数是多少?
如图所示，由均匀导线制成的半径为R的圆环，以速度v匀速进入一磁感应强度大小为B的匀强磁场。当圆环运动到图示位置(∠aOb = 90°)时，a、b两点的电势差为多少?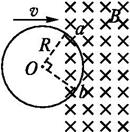
如图所示，静置于水平地面的三辆手推车沿一直线排列，质量均为m，人在极端的时间内给第一辆车一水平冲量使其运动，当车运动了距离L时与第二辆车相碰，两车以共同速度继续运动了距离L时与第三车相碰，三车以共同速度又运动了距离L时停止。车运动时受到的摩擦阻力恒为车所受重力的k倍，重力加速度为g,若车与车之间仅在碰撞时发生相互作用，碰撞时间很短，忽略空气阻力，求：
(1)整个过程中摩擦阻力 所做的总功；
(2)人给第一辆车水平冲量的大小；
(3)第一次与第二次碰撞系统功能损失之比。
用初动能为E1=0.6MeV的质子轰击静止锂核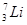
生成2个α粒子．己知质子质量mp=1.0078u，α粒子的质量 ma="4.0026" u，锂核质量mLi="7.0160" u，质子的质量mH="1.0078" u，．试回答下列问题(1 u相当于931.5MeV)
(1)写出核反应方程式
(2)核反应中释放出的能量ΔE
(3)核反应释放的能量全部用来增加了两个α粒子的动能，则核反应后两个α粒子具有总动能是多少?
如图所示，木板长为2m，质量是为2Kg，静止于光滑的水平面上，木块质量为4Kg（可看成质点），它与木板之间摩擦因数是0.3，要使它在木块上从左端滑到右端而不致滑落，则木块初速度的最大值是多少？