(本小题满分12分)
已知数列 中,
中, (
( 为常数),
为常数),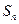 为
为 的前
的前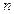 项和,且
项和,且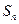 是
是 与
与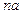 的等差中项.
的等差中项.
(Ⅰ)求 并归纳出
并归纳出 (不用证明);
(不用证明);
(Ⅱ)若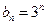 且
且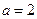 ,求数列
,求数列 的前
的前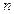 项和
项和 .
.
已知二次函数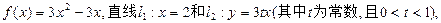
直线l2与函数 的图象以及直线l1、l2与函数
的图象以及直线l1、l2与函数 的图象所围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为
的图象所围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为
(I)求函数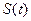 的解析式;
的解析式;
(II)定义函数 的三条切线,求实数m的取值范围。
的三条切线,求实数m的取值范围。
|
如图,在以点O为圆心,AB为直径的半圆中,D为半圆弧的中点, P为半圆弧上一点,且AB=4,∠POB=30°,双曲线C以A,B为焦点且经过点P.
(Ⅰ)建立适当的平面直角坐标系,求双曲线C的方程;
(Ⅱ)设过点D的直线l与双曲线C相交于不同两点E、F,
若△OEF的面积不小于2 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.
已知数列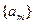 是首项为,公差为
是首项为,公差为 的等差数列,
的等差数列, 是首项为
是首项为 ,公比为的等比数列,且满足
,公比为的等比数列,且满足 ,其中
,其中 .
.
(Ⅰ)求a的值
(Ⅱ)若数列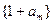 与数列
与数列 有公共项,将所有公共项按原顺序排列后构成一个新数列
有公共项,将所有公共项按原顺序排列后构成一个新数列 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅲ)记(Ⅱ)中数列 的前项之和为
的前项之和为 ,求证:
,求证: .
.
如果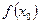 是函数
是函数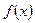 的一个极值,称点
的一个极值,称点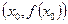 是函数
是函数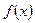 的一个极值点.已知函数
的一个极值点.已知函数
(1)若函数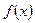 总存在有两个极值点
总存在有两个极值点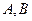 ,求
,求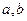 所满足的关系;
所满足的关系;
(2)若函数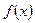 有两个极值点
有两个极值点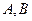 ,且存在
,且存在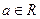 ,求
,求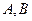 在不等式
在不等式 表示的区域内时实数
表示的区域内时实数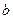 的范围.
的范围.
(3)若函数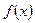 恰有一个极值点
恰有一个极值点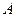 ,且存在
,且存在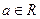 ,使
,使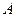 在不等式
在不等式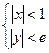 表示的区域内,证明:
表示的区域内,证明: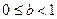 .
.
已知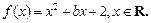
(1)若函数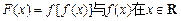 时有相同的值域,求b的取值范围;
时有相同的值域,求b的取值范围;
(2)若方程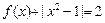 在(0,2)上有两个不同的根x1、x2,求b的取值范围,并证明
在(0,2)上有两个不同的根x1、x2,求b的取值范围,并证明