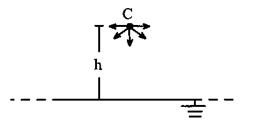
如图所示,某空间有一竖直向下的匀强电场,电场强度E=1.0×102V/m,一块足够大的接地金属板水平放置在匀强电场中,在金属板的正上方高度h=0.80m的C处有一粒子源,可在纸面内向水平线以下的各个方向均匀放出带电粒子,带电粒子的初速度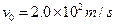 ,质量为
,质量为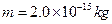 ,电荷量为
,电荷量为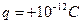 ,粒子最终落在金属板上。若不计粒子重力,求:
,粒子最终落在金属板上。若不计粒子重力,求:
(1)粒子源所在处C点的电势;
(2)带电粒子打在金属板上时的动能;
(3)若只将电场换为匀强磁场,磁场分布在半径为力,圆心在C点的圆形区域内,磁场方向垂直纸面向里,磁感应强度为B=0.5T,从粒子源射出的粒子打在金属板上的范围。(结果保留两位有效数字,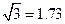 )
)
运动员驾驶摩托车做腾跃特技表演是一种刺激性很强的运动项目。如图所示,AB是水平路面,BC是半径为20m的圆弧,CDE是一段曲面。运动员驾驶功率始终是P=1.8 kW的摩托车在AB段加速,通过B点时速度已达到最大vm=20m/s,再经t=13s的时间通过坡面到达E点,此刻关闭发动机水平飞出。已知人和车的总质量m=180 kg,坡顶高度h=5m,落地点与E点的水平距离s=16m,重力加速度g=10m/s2。如果在AB段摩托车所受的摩擦阻力恒定,且不计空气阻力,求:
(1)AB段摩托车所受摩擦阻力的大小
(2)摩托车过圆弧B点时受到地面支持力的大小
(3)摩托车在沿BCDE冲上坡顶冲上坡顶的过程中克服摩擦阻力做的功
中国自行研制,具有完全自主知识产权的“神舟号”飞船,目前已经达到或优于国际第三代载人飞船技术,其发射过程简化如下:飞船在酒泉卫星发射中心发射,由长征运载火箭送入近地点为A、远地点为B的椭圆轨道上,A点距地面的高度为h1,飞船飞行五周后进行变轨,进入预定圆轨道,如图所示,设飞船在预定圆轨道上飞行n圈所用时间为t,若已知地球表面重力加速度为g,地球半径为R,已知万有引力常量G,求:
⑴地球的平均密度是多少
⑵飞船经过椭圆轨道近地点A时的加速度大小
⑶椭圆轨道远地点B距地面的高度
2014年11月22日16时55分,四川省康定县境内发生6.3级地震并引发一处泥石流。一汽车停在小山坡底,突然司机发现山坡上距坡底240 m处的泥石流以8 m/s的初速度,0.4 m/s2的加速度匀加速倾泻而下。假设泥石流到达坡底后速率不变,在水平地面上做匀速直线运动,司机的反应时间为1s,汽车启动后以恒定的加速度一直做匀加速直线运动。其过程简化为下图所示,求:
(1)泥石流到达坡底的时间和速度大小?
(2)试通过计算说明:汽车的加速度至少多大才能脱离危险?(结果保留三位有效数字)
如图所示,一不可伸长的轻绳上端悬挂于O点,下端系一质量m=1.0 kg的小球。现将小球拉到A点(保持绳绷直)由静止释放,当它经过B点时绳恰好被拉断,小球平抛后落在水平地面上的C点。地面上的D点与OB在同一竖直线上,已知绳长L=1.0 m,B点离地高度H=1.0 m,A、B两点的高度差h=0.5 m,重力加速度g取10 m/s2,不计空气影响,求:
(1)地面上DC两点间的距离s;
(2)轻绳所受的最大拉力大小。
一直升机以5.0 m/s的速度竖直上升,某时刻从飞机上释放一物块,经2.0 s落到地面上,不计空气阻力,g取10 m/s2。求:
(1)物块落到地面时的速度大小;
(2)物块在2.0 s内通过的路程;
(3)物块释放时距地面的高度。