(本大题满分12分)
给出定义在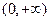 上的三个函数:
上的三个函数: ,已知
,已知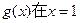 处取极值.
处取极值.
(I)确定函数 的单调性;
的单调性;
(II)求证:当 成立.
成立.
(III)把函数 的图象向上平移6个单位得到函数
的图象向上平移6个单位得到函数 的图象,试确定函数
的图象,试确定函数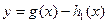 的零点个数,并说明理由。
的零点个数,并说明理由。
(本小题满分7分)选修4-2:矩阵与变换
已知矩阵 .
.
(1)矩阵 对应的变换把直线
对应的变换把直线
 变为直线
变为直线 ,求直线
,求直线 的方程;
的方程;
(2)求 的逆矩阵
的逆矩阵 .
.
(本小题满分14分)已知函数 (
( ).
).
(1)若 为函数
为函数 的极值点,求
的极值点,求 的值;
的值;
(2)若 ,
, 已知
已知
 ,
,
 ,若直线
,若直线 、
、 及直线
及直线 与函数
与函数 的图象所围成的封闭图形如阴影部分所示,求阴影面积
的图象所围成的封闭图形如阴影部分所示,求阴影面积 关于
关于 的函数
的函数 的最小值
的最小值 ;
; 证明不等式:
证明不等式: .
.
(本小题满分13分)已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆 过点
过点 ,离心率
,离心率 .
.
(1)求椭圆 的方程;
的方程;
(2)如图,动直线
 与椭圆
与椭圆 有且仅有一个公共点,
有且仅有一个公共点, 求
求 ,
, 满足的关系式;
满足的关系式; 如图,
如图, 、
、 为椭圆
为椭圆 的左、右焦点,作
的左、右焦点,作 ,
, ,垂足分别为
,垂足分别为 、
、 ,四边形
,四边形 的面积
的面积 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
(本小题满分13分)如图1,在 中,
中, ,
, ,
, ,
, 、
、 分别为
分别为 、
、 的中点,连接
的中点,连接 并延长交
并延长交 于
于 ,将
,将 沿
沿 折起,使平面
折起,使平面 平面
平面 ,如图2所示.
,如图2所示.
(1)求证: 平面
平面 ;
;
(2)求平面 与平面
与平面 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(3)在线段 上是否存在点
上是否存在点 使得
使得 平面
平面 ?若存在,请指出点
?若存在,请指出点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
(本小题满分13分)根据新修订的《环境空气质量标准》指出空气质量指数在 ,各类人群可正常活动.某市环保局在2014年对该市进行为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
,各类人群可正常活动.某市环保局在2014年对该市进行为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为 ,
, ,
, ,
, ,
, ,由此得到样本的空气质量指数频率分布直方图,如图.
,由此得到样本的空气质量指数频率分布直方图,如图.
(1)求 的值;
的值;
(2)根据样本数据,试估计这一年度的空气质量指数的平均值;
(3)用这50个样本数据来估计全年的总体数据,将频率视为概率.如果空气质量指数不超过20,就认定空气质量为“最优等级”.从这一年的监测数据中随机抽取2天的数值,其中达到“最优等级”的天数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.