(本小题满分12分)
在一个盒子中放有标号分别为1、2、3的三张卡片,现从这个盒子中有放回地先后抽取两张卡片,并记它们的标号分别为 ,设
,设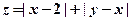 ,
,
(1)求事件“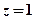 ”发生的概
”发生的概 率;
率;
(2)求 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率。
取得最大值”的概率。
(本小题满分12分)
已知 是公差为正数的等差数列,首项
是公差为正数的等差数列,首项 ,前n项和为Sn,数列
,前n项和为Sn,数列 是等比数列,首项
是等比数列,首项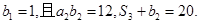
(1)求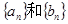 的通项公式.
的通项公式.
(2)令 的前n项和Tn.
的前n项和Tn.
.(本小题满分12分)
已知函数
(1)求函数 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)△ABC内角A、B、C的对边长分别为a、b、c,若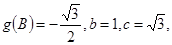
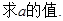
(本小题满分14分)
已知一非零向量列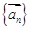 满足:
满足: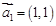 ,
,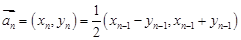
 .
.
(1)证明: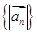 是等比数列;
是等比数列;
(2)设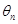 是
是 的夹角
的夹角 ,
,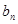 =
=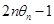 ,
, ,求
,求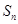 ;
;
(3)设
 ,问数列
,问数列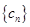 中是否存在最小项?若存在,求出最小值;若不存在,请说明理由.
中是否存在最小项?若存在,求出最小值;若不存在,请说明理由.
已知函数 ,
,
(1)求 的最小值;
的最小值;
(2)若对所有 都有
都有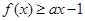 ,求实数
,求实数 的取值范围.
的取值范围.
(本题满分12分)
某商店经销一种洗衣粉,年销售总量为6000包,每包进价为2.8元,销售价为3.4元,全年分若干次进货,每次进货均为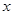 包,已知每次进货的运输劳务费为62.5元,全部洗衣粉一年的保管费为1.5
包,已知每次进货的运输劳务费为62.5元,全部洗衣粉一年的保管费为1.5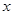 元.
元.
(1)将该商店经销洗衣粉一年的利润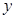 (元)表示为每次进货量
(元)表示为每次进货量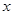 (包)的函数;
(包)的函数;
(2)为使利润最大,每次应进货多少包?