把边长为60cm的正方形铁皮的四角切去边长为xcm的相等的正方形,然后折成一个高度为xcm的无盖的长方体的盒子,问x取何值时,盒子的容积最大,最大容积是多少?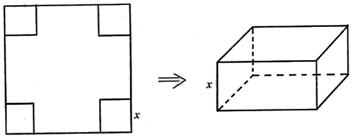
(本小题满分12分)
某商店储存的50个灯泡中, 甲厂生产的灯泡占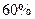 , 乙厂生产的灯泡占
, 乙厂生产的灯泡占 , 甲厂生产的灯泡的一等品率是
, 甲厂生产的灯泡的一等品率是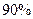 , 乙厂生产的灯泡的一等品率是
, 乙厂生产的灯泡的一等品率是 .
.
(1) 若从这50个灯泡中随机抽取出一个灯泡(每个灯泡被取出的机会均等), 则它是甲厂生产的一等品的概率是多少?
(2) 从这50个灯泡中随机抽取出的一个灯泡是一等品, 求它是甲厂生产的概率是 多少?
多少?
(3) 若从这50个灯泡中随机抽取出两个灯泡(每个灯泡被取出的机会均等), 这两个灯泡中是甲厂生产的一等品的个数记为 , 求
, 求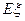 的值.
的值.
(本小题满分12分)
如图所示的多面体,它的正视图为直角三角形,侧视图为矩形,俯视图为直角梯形(尺寸如图所示).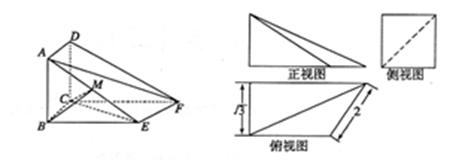
(1) 求证:AE∥平面DCF
(2) 当AB的长为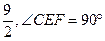 时,
时,
求二面角A-EF-C的大小.
(本小题满分12分)
如图,A是单位圆与 轴正半轴的交点,点P在单位圆上,∠AOP=
轴正半轴的交点,点P在单位圆上,∠AOP=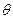 (0<
(0<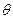 <
< ),
),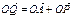 ,四边形OAQP的面积为S.
,四边形OAQP的面积为S.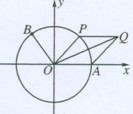
(1) 求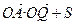 的最大值及此时
的最大值及此时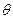 的值
的值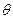 0.
0.
(2) 设点B的坐标为( ),∠AOB=
),∠AOB= ,在(1)的条件下,
,在(1)的条件下,
求△BOP的面积S0.
.(本小题满分14分)
在平面直角坐标系上,设不等式组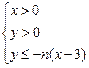 (
(
 )所表示的平面区域为
)所表示的平面区域为 ,记
,记 内的整点(即横坐标和纵坐标均为整数的点)的个数为
内的整点(即横坐标和纵坐标均为整数的点)的个数为 .(Ⅰ)求
.(Ⅰ)求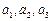 并猜想
并猜想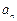 的表达式再用数学归纳法加以证明;(Ⅱ)设数列
的表达式再用数学归纳法加以证明;(Ⅱ)设数列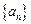 的前r项和为
的前r项和为 ,数列
,数列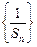 的前r项和
的前r项和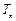 ,是否存在自然数m?使得对一切
,是否存在自然数m?使得对一切 ,
, 恒成立。若存在,求出m的值,若不存在,请说明理由。
恒成立。若存在,求出m的值,若不存在,请说明理由。
.(本小题满分14分)
已知函数 是函数
是函数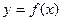 的极值点.
的极值点.
(1)求实数 的值;
的值;
(2)若方程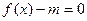 有两个不相等的实数根,求实数m的取值.
有两个不相等的实数根,求实数m的取值.