(本小题满分12分)在一个选拔项目中,每个选手都需要进行4轮考核,每轮设有一个问
题,能正确回答者进入下一轮考核,否则被淘汰。已知某选手能正确回答第一、二、三、
四轮问题的概率分别为 、
、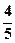 、
、 、
、 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(Ⅰ)求该选手进入第三轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率;
设函数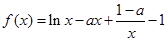 .
.
(Ⅰ)当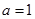 时,求曲线
时,求曲线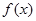 在
在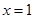 处的切线方程;
处的切线方程;
(Ⅱ)当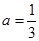 时,求函数
时,求函数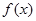 的单调区间;
的单调区间;
(Ⅲ)在(Ⅱ)的条件下,设函数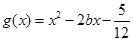 ,若对于
,若对于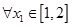 ,
,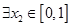 ,使
,使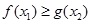 成立,求实数
成立,求实数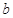 的取值范围.
的取值范围.
已知函数 的图象与
的图象与 的图象关于直线
的图象关于直线 对称。
对称。
(Ⅰ)若直线 与
与 的图像相切, 求实数
的图像相切, 求实数 的值;
的值;
(Ⅱ)判断曲线 与曲线
与曲线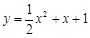 公共点的个数.
公共点的个数.
(Ⅲ)设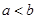 ,比较
,比较 与
与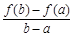 的大小, 并说明理由.
的大小, 并说明理由.
已知函数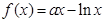 ,
,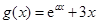 ,其中
,其中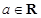 .
.
(Ⅰ)求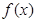 的极值;
的极值;
(Ⅱ)若存在区间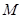 ,使
,使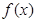 和
和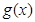 在区间
在区间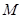 上具有相同的单调性,求
上具有相同的单调性,求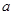 的取值范围.
的取值范围.
已知函数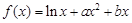 (其中
(其中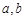 为常数且
为常数且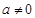 )在
)在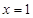 处取得极值.
处取得极值.
(I) 当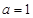 时,求
时,求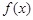 的单调区间;
的单调区间;
(II) 若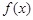 在
在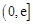 上的最大值为
上的最大值为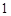 ,求
,求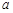 的值.
的值.
已知函数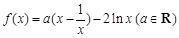 .
.
(Ⅰ)若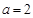 ,求曲线
,求曲线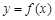 在点
在点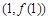 处的切线方程;
处的切线方程;
(Ⅱ)求函数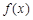 的单调区间;
的单调区间;
(Ⅲ)设函数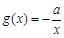 .若至少存在一个
.若至少存在一个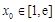 ,使得
,使得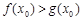 成立,求实数
成立,求实数 的取值范围.
的取值范围.