(本小题满分12分)
2009年我市城市建设取得最大进展的一年,正式拉开了从“两湖”时代走向“八里湖”时代的大幕。为了建设大九江的城市框架,市政府大力发展“八里湖”新区,现有甲乙两个项目工程待建,请三位专家独立评审。假设每位专家评审结果为“支持”或“不支持”的概率都是 ,每个项目每获得一位专家“支持”则加1分,“不支持”记为0分,令
,每个项目每获得一位专家“支持”则加1分,“不支持”记为0分,令 表示两个项目的得分总数。
表示两个项目的得分总数。 (1)求甲项目得1分乙项目得2分的概率;
(1)求甲项目得1分乙项目得2分的概率;
(2)求 的数学期望E
的数学期望E 。
。
(本小题满分10分)
在盒子里有大小相同,仅颜色不同的乒乓球共10个,其中红球5个,白球3个,蓝球2个.现从中任取出一球确定颜色后放回盒子里,再取下一个球.重复以上操作,最多取3次,过程中如果取出蓝色球则不再取球. 求:
(1)最多取两次就结束的概率;
(2)整个过程中恰好取到2个白球的概率;
(本小题14分)设函数

(1)若 时函数
时函数 有三个互不相同的零点,求
有三个互不相同的零点,求 的范围;
的范围;
(2)若函数 在
在 内没有极值点,求
内没有极值点,求 的范围;
的范围;
(3)若对任意的 ,不等式
,不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
(本小题13分)已知定点 及椭圆
及椭圆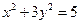 ,过点
,过点 的动直线与该椭圆相交于
的动直线与该椭圆相交于 两点.
两点.
(1)若线段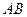 中点的横坐标是
中点的横坐标是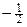 ,求直线
,求直线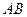 的方程;
的方程;
(2)在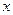 轴上是否存在点
轴上是否存在点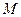 ,使
,使 为常数?若存在,求出点
为常数?若存在,求出点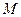 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
(本小题12分)已知数列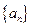 的前
的前 项和
项和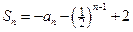 (
( 为正整数)
为正整数)
(1)求数列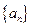 的通项公式;
的通项公式;
(2)若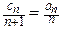 ,
,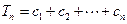 ,求
,求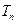 .
.
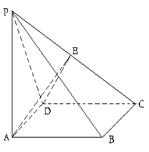
(本小题12分)如图,四棱椎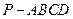 的底面为菱形,且
的底面为菱形,且 ,
,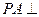 平面
平面 ,
, ,
,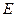 为
为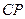 的中点.
的中点.
(1)求直线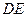 与平面
与平面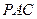 所成角的正切值;
所成角的正切值;
(2)在线段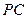 上是否存在一点
上是否存在一点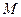 ,使
,使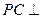 面
面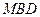 成立?如果存在,求出
成立?如果存在,求出 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.