设数列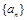 的前
的前 项和为
项和为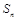 ,且满足
,且满足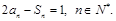
(1)求数列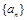 的通项公式;
的通项公式;
(2)在数列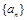 的每两项之间都按照如下规则插入一些数后,构成新数列
的每两项之间都按照如下规则插入一些数后,构成新数列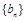 ,在
,在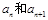 两项之间插入
两项之间插入 个数,使这
个数,使这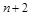 个数构成等差数列,求
个数构成等差数列,求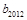 的值;
的值;
(3)对于(2)中的数列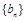 ,若
,若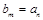 ,并求
,并求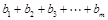 (用
(用 表示).
表示).
一个盒子中装有分别标有数字1、2、3、4的4个大小、形状完全相同的小球,现从中有放回地随机抽取2个小球,抽取的球的编号分别记为 、
、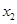 ,记
,记 .
.
(Ⅰ)求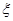 取最大值的概率;
取最大值的概率;
(Ⅱ)求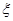 的分布列及数学期望.
的分布列及数学期望.
已知抛物线 ,点P(-1,0)是其准线与
,点P(-1,0)是其准线与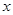 轴的焦点,过P的直线
轴的焦点,过P的直线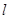 与抛物线C交于A、B两点.
与抛物线C交于A、B两点.
(1)当线段AB的中点在直线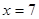 上时,求直线
上时,求直线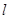 的方程;
的方程;
(2)设F为抛物线C的焦点,当A为线段PB中点时,求△FAB的面积.
四棱锥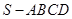 中,底面
中,底面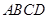 为平行四边形,侧面
为平行四边形,侧面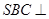 底面
底面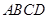 .已知
.已知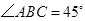 ,
,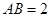 ,
,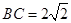 ,
,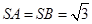 .
.
(Ⅰ)证明 ;
;
(Ⅱ)求直线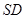 与平面
与平面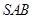 所成角的正弦值.
所成角的正弦值.
已知函数
(Ⅰ)若 ,求
,求 的极大值;
的极大值;
(Ⅱ)若 在定义域内单调递减,求满足此条件的实数k的取值范围.
在定义域内单调递减,求满足此条件的实数k的取值范围.
已知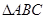 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,
, 是锐角,且
是锐角,且 .
.
(Ⅰ)求 的度数;
的度数;
(Ⅱ)若 ,
,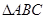 的面积为
的面积为 ,求
,求 的值.
的值.