(本小题满分12分)
经调查某 校高三年级学生家庭月平均收入不多于10000元的共有100
校高三年级学生家庭月平均收入不多于10000元的共有100 0人,统计这些学生家庭月平均收入情况,得到家庭月平均收入频率分布直方图如图所示.
0人,统计这些学生家庭月平均收入情况,得到家庭月平均收入频率分布直方图如图所示.
某企业准备给该校高三学生发放助学金,发放规定为:家庭收入在4000元以下(≤4000元)的每位同学得助学金2000元,家庭收入在 (元)间的每位同学得助学金1500元,家庭收入在
(元)间的每位同学得助学金1500元,家庭收入在 (元)间的每位同学得助学金1000元,家庭收入在
(元)间的每位同学得助学金1000元,家庭收入在 (元)间的同学不发助学金.
(元)间的同学不发助学金.
(l)记该年级某位同学所得助学金为 元,写出
元,写出 的分布列,并计算该企业发放该年级的助学金约需要的资金;
的分布列,并计算该企业发放该年级的助学金约需要的资金;
(2)记该年级两位同学所得助学金之差的绝对值为 元,求
元,求 .
.
已知函数 的定义域为集合
的定义域为集合 ,
, .
.
(1)若 ,求
,求 的取值范围;
的取值范围;
(2)若全集 ,
, ,求
,求 及
及 .
.
已知数列 的前n项和为
的前n项和为 ,且满足
,且满足 ,
, ,
,
(1)设 ,数列
,数列 为等比数列,求实数
为等比数列,求实数 的值;
的值;
(2)设 ,求数列
,求数列 的通项公式;
的通项公式;
(3)令 ,求数列
,求数列 的前n项和
的前n项和 .
.
已知抛物线 的焦点为
的焦点为 ,准线为
,准线为 ,过
,过 上一点P作抛物线的两切线,切点分别为A、B,
上一点P作抛物线的两切线,切点分别为A、B,
(1)求证: ;
;
(2)求证:A、F、B三点共线;
(3)求 的值.
的值.
已知函数 为奇函数,
为奇函数,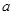 为常数,
为常数,
(1)求实数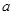 的值;
的值;
(2)证明:函数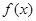 在区间
在区间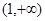 上单调递增;
上单调递增;
(3)若对于区间 上的每一个
上的每一个 值,不等式
值,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
连续抛两次质地均匀的骰子得到的点数分别为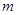 和
和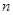 ,将
,将 作为Q点的横、纵坐标,
作为Q点的横、纵坐标,
(1)记向量 的夹角为
的夹角为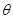 ,求
,求 的概率;
的概率;
(2)求点Q落在区域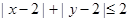 内的概率.
内的概率.