写出用更相减损之术求a、b最大公约数的程序.
(本小题14分)设函数

(1)若 时函数
时函数 有三个互不相同的零点,求
有三个互不相同的零点,求 的范围;
的范围;
(2)若函数 在
在 内没有极值点,求
内没有极值点,求 的范围;
的范围;
(3)若对任意的 ,不等式
,不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
(本小题13分)已知定点 及椭圆
及椭圆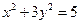 ,过点
,过点 的动直线与该椭圆相交于
的动直线与该椭圆相交于 两点.
两点.
(1)若线段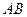 中点的横坐标是
中点的横坐标是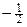 ,求直线
,求直线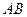 的方程;
的方程;
(2)在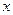 轴上是否存在点
轴上是否存在点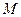 ,使
,使 为常数?若存在,求出点
为常数?若存在,求出点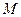 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
(本小题12分)已知数列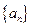 的前
的前 项和
项和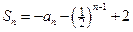 (
( 为正整数)
为正整数)
(1)求数列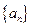 的通项公式;
的通项公式;
(2)若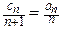 ,
,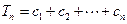 ,求
,求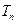 .
.
(本小题12分)如图,四棱椎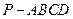 的底面为菱形,且
的底面为菱形,且 ,
,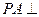 平面
平面 ,
, ,
,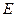 为
为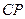 的中点.
的中点.
(1)求直线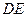 与平面
与平面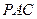 所成角的正切值;
所成角的正切值;
(2)在线段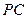 上是否存在一点
上是否存在一点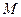 ,使
,使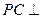 面
面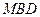 成立?如果存在,求出
成立?如果存在,求出 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.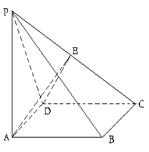
(本小题12分)某校设计了一个实验学科的实验考察方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作。规定:至少正确完成其中2题的便可通过考察,已知6道备选题中考生甲有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是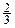 ,且每题正确完成与否互不影响。求:
,且每题正确完成与否互不影响。求:
(1)分别写出甲、乙两个考生正确分析完成题数的概率分布列;
(2)分析哪个考生通过考察的概率较大?