(本小题满分12分)贵广高速铁路自贵阳北站起,经黔南州、黔东南、广西桂林、贺州、广东肇庆、佛山终至广州南站. 其中广东省内有怀集站、广宁站、肇庆东站、三水南站、佛山西站、广州南站共6个站. 记者对广东省内的6个车站的外观进行了满意度调查,得分情况如下:
| 车站 |
怀集站 |
广宁站 |
肇庆东站 |
三水南站 |
佛山西站 |
广州南站 |
| 满意度得分 |
70 |
76 |
72 |
70 |
72 |
x |
已知6个站的平均得分为75分.
(1)求广州南站的满意度得分x,及这6个站满意度得分的标准差;
(2)从广东省内前5个站中,随机地选2个站,求恰有1个站得分在区间(68,75)中的概率.
已知a= ,c=2,B=150°,求边b的长及
,c=2,B=150°,求边b的长及
设函数 是定义在
是定义在 上的减函数,并且满足
上的减函数,并且满足 ,
,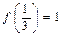 ,
,
(1)求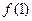 ,
,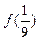 ,
, 的值, (2)如果
的值, (2)如果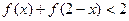 ,求x的取值范围。
,求x的取值范围。
(满分12分) 某商店按每件80元的价格,购进商品1000件(卖不出去的商品将成为废品);市场调研推知:当每件售价为100元时,恰好全部售完;当售价每提高1元时,销售量就减少5件;为获得最大利润,商店决定提高售价 元,获得总利润
元,获得总利润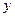 元.
元.
(1)请将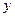 表示为
表示为 的函数;
的函数;
(2)当售价为多少时,总利润取最大值,并求出此时的利润.
函数 是R上的偶函数,且当
是R上的偶函数,且当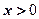 时,函数的解析式为
时,函数的解析式为
(1)求 的值;
的值;
(2)用定义证明 在
在 上是减函数;
上是减函数;
(3)求当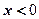 时,函数的解析式;
时,函数的解析式;
已知二次函数的图象如图所示.
(1)写出该函数的零点;
(2)写出该函数的解析式.
(3)求当x∈ 时,函数的值域.
时,函数的值域.