(本小题满分12分)
某校从参加某次“广州亚运”知识竞赛测试的学生中随机抽出 名学生,将其成绩(百分制)(均为整数)分成六段
名学生,将其成绩(百分制)(均为整数)分成六段 ,
, …
…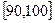 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求分数在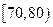 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的
平均分;
(Ⅲ)若从 名学生中
名学生中 随机抽取
随机抽取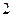 人,抽到的学生成绩在
人,抽到的学生成绩在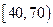 记
记 分,在
分,在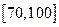 记
记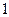 分,用
分,用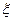 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求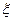 的分布列和数学期望.
的分布列和数学期望.
已知向量 ,设函数 ,求函数 的最小正周期及 时的最大值.
某种汽车,购车费用是10万元,每年使用的保险费和汽油费为 万元,年维修费第一年为
万元,年维修费第一年为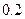 万元,以后逐年递增
万元,以后逐年递增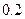 万元,问这种汽车使用多少年时,它的年平均费用最少? (12分)
万元,问这种汽车使用多少年时,它的年平均费用最少? (12分)
在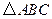 中,内角
中,内角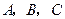 对边的边长分别是
对边的边长分别是 ,且
,且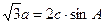 ,
,
(1)求角 (2)若边
(2)若边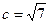 且
且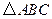 的面积等于
的面积等于 ,求
,求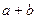 的值.(12分)
的值.(12分)
解关于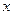 的不等式:
的不等式: .
. (12分)
(12分)
(本题10分)甲、乙两人各射击一次,击中目标的概率分别是 和
和 .假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间也没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间也没有影响.
(Ⅰ)求甲射击4次,至少1次未击中目标的概率;
(Ⅱ)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(Ⅲ)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少?