(本小题满分12 分)
分)
设函数f(x)的定义域为R,若|f(x)|≤|x|对任意的实数x均成立,则称函数f(x)为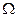 函数。
函数。
(1)试判断函数 =
=
 =
=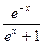 中哪些是
中哪些是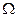 函数,并说明理由;
函数,并说明理由;
(2)求证:若a>1,则函数f(x)=ln(x2+a)-lna是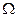 函数。
函数。
辽宁广播电视塔位于沈阳市沈河区青年公园西侧,蜿蜒的南运河带状公园内,占地8000平方米.全塔分为塔座、塔身、塔楼和桅杆四部分. 某数学活动小组在青年公园的A处测得塔顶B处的仰角为45°,在地面上,沿着A点与塔底中心C处连成的直线行走129米后到达D处(假设可以到达),此时测得塔顶B处的仰角为60°.
(1)请你根据题意,画出一个ABCD四点间的简单关系图形;
(2)根据测量结果,计算辽宁广播电视塔的高度(精确到1米).
解关于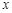 的一元二次不等式
的一元二次不等式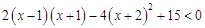 .
.
已知函数 (
( ).
).
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)若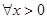 ,不等式
,不等式 恒成立,求实数
恒成立,求实数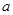 的取值范围.
的取值范围.
已知抛物线 的顶点在坐标原点
的顶点在坐标原点 ,对称轴为
,对称轴为 轴,焦点为
轴,焦点为 ,抛物线上一点
,抛物线上一点 的横坐标为2,且
的横坐标为2,且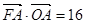 .
.
(1)求抛物线的方程;
(2)过点 作直线
作直线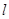 交抛物线于
交抛物线于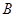 ,
, 两点,求证:
两点,求证: .
.
已知离心率 的椭圆
的椭圆 一个焦点为
一个焦点为 .
.
(1)求椭圆 的方程;
的方程;
(2) 若斜率为1的直线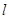 交椭圆
交椭圆 于
于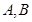 两点,且
两点,且 ,求直线
,求直线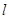 方程.
方程.