已知抛物线
的顶点在坐标原点
，对称轴为
轴，焦点为
,抛物线上一点
的横坐标为2，且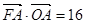
.
(1)求抛物线的方程；
(2)过点
作直线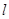
交抛物线于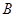
，两点,求证:
.
如图，在△
中，
是
的中点，
是
的中点，
的延长线交
于
.
（Ⅰ）求
的值；
（Ⅱ）若△
的面积为
， 四边形
的面积为
，求
的值．
已知函数
（常数
）.
（Ⅰ）求
的单调区间；
（Ⅱ）设
如果对于的图象上两点
，存在
，使得的图象在
处的切线
∥
，求证：
.
已知
分别为椭圆
的上下焦点，其中
也是抛物线
的焦点，点
是
与
在第二象限的交点，且
.
（1）求椭圆的方程；
（2）已知点
和圆
，过点
的动直线
与圆
相交于不同的两
点
，在线段
上取一点
,满足
且
.
求证：点总在某定直线上.
如图，在三棱拄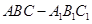
中，
侧面
，已知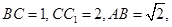
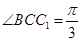
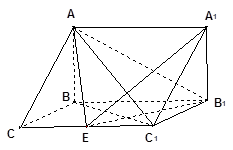
（1）求证：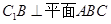
；
（2）、当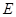
为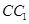
的中点时，求二面角
的平面角的正切值.
某校的学生记者团由理科组和文科组构成，具体数据如下表所示：
| 组别 |
理科 |
文科 |
||
| 性别 |
男生 |
女生 |
男生 |
女生 |
| 人数 |
4 |
4 |
3 |
1 |
学校准备从中选出4人到社区举行的大型公益活动进行采访，每选出一名男生，给其所在小组记1分，每选出一名女生则给其所在小组记2分，若要求被选出的4人中理科组、文科组的学生都有．(Ⅰ)求理科组恰好记4分的概率？
(Ⅱ)设文科男生被选出的人数为
，求随机变量的分布列和数学期望
．