(本小题满分13分)
已知等比数列 的公比
的公比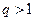 ,
,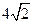 是
是 和
和 的一个等比中项,
的一个等比中项,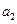 和
和 的等差中项为
的等差中项为 ,若数列
,若数列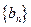 满足
满足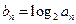 (
(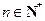 ).
).
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前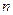 项和
项和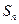 .
.
已知定义域为R的函数f(x)为奇函数,且满足f(x+2)=-f(x),当x∈[0,1]时,f(x)=2x-1.
(1)求f(x)在[-1,0)上的解析式;
(2)求f(log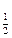 24).
24).
已知函数f(x)=loga(x+1)(a>1),若函数y=g(x)图象上任意一点P关于原点对称点Q的轨迹恰好是函数f(x)的图象.
(1)写出函数g(x)的解析式;
(2)当x∈[0,1)时总有f(x)+g(x)≥m成立,求m的取值范围.
已知函数f(x)=log2(x2-ax-a)在区间(-∞,1-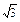 ]上是单调递减函数.求实数a的取值范围.
]上是单调递减函数.求实数a的取值范围.
已知f(x)= .
.
(1)判断函数的奇偶性;
(2)证明:f(x)是定义域内的增函数;
(3)求f(x)的值域.
已知定义在R上的奇函数f(x)有最小正周期2,且当x∈(0,1)时,f(x)= .
.
(1)求f(x)在[-1,1]上的解析式;
(2)证明:f(x)在(0,1)上是减函数.