如图,我市有一个健身公园,由一个直径为2km的半圆和一个以 为斜边的等腰直角三角形
为斜边的等腰直角三角形 构成,其中
构成,其中 为
为 的中点.现准备在公园里建设一条四边形健康跑道
的中点.现准备在公园里建设一条四边形健康跑道 ,按实际需要,四边形
,按实际需要,四边形 的两个顶点
的两个顶点 分别在线段
分别在线段 上,另外两个顶点
上,另外两个顶点 在半圆上,
在半圆上, 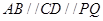 ,且
,且 间的距离为1km.设四边形
间的距离为1km.设四边形 的周长为
的周长为 km.
km.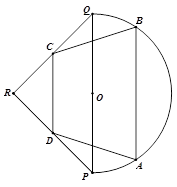
(1)若 分别为
分别为 的中点,求
的中点,求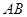 长;
长;
(2)求周长 的最大值.
的最大值.
【原创】(本小题共13分)已知函数 ,
, ,其中
,其中 ,
, 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当 时,求函数
时,求函数 的极小值;
的极小值;
(Ⅱ)对 ,是否存在
,是否存在 ,使得
,使得 成立?若存在,求出
成立?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题共12分)已知数列 满足a1=1,an>0,Sn是数列
满足a1=1,an>0,Sn是数列 的前n项和,对任意的
的前n项和,对任意的
n∈N*,有2Sn=2an2+an-1.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)记 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
【原创】(本小题共12分)2015年清明期间,某高速公路车辆较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(km/h)分成七段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),[90,95)后得到如图所示的频率分布直方图,据图解答下列问题:
(Ⅰ)求a的值,并说明交警部门采用的是什么抽样方法?
(Ⅱ)求这120辆车行驶速度的众数和中位数的估计值(精确到0.1);
(Ⅲ)若该路段的车速达到或超过90km/h即视为超速行驶,试根据样本估计该路段车辆超速行驶的概率.
(本小题共13分)如图所示,在正方体 中,
中, 分别是棱
分别是棱 的中点.
的中点.
(Ⅰ)证明:平面 平面
平面 ;
;
(Ⅱ)证明: //平面
//平面 ;
;
(Ⅲ)若正方体棱长为1,求四面体 的体积.
的体积.
【改编】(本小题共12分)已知 ,
, ,且
,且 .
.
(Ⅰ)求函数 的周期;
的周期;
(Ⅱ)当 时,
时, 的最小值是-4,求此时函数
的最小值是-4,求此时函数 的最大值,及相应的
的最大值,及相应的 的值.
的值.