(本小题满分15分)
在参加市里主办的科技知识竞赛的学生中随机选取了40名学生的成绩作为样本,这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式 分成6组:第一组,成绩大于等于40分且小于50分;第二组,成绩大于等于50分且小于60分;……第六组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图。
分成6组:第一组,成绩大于等于40分且小于50分;第二组,成绩大于等于50分且小于60分;……第六组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图。
在选取的40名学生中。
(I)求成绩在区间 内的学生人数;
内的学生人数;
(II)从成绩大于等于80分的学生中随机选2名学生,求至少有1名学生成绩在区间[90,100]内的概率。
已知圆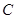 的参数方程为
的参数方程为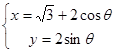 (
( 为参数),
为参数),
(1)以原点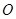 为极点、
为极点、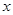 轴的正半轴为极轴建立极坐标系,写出圆
轴的正半轴为极轴建立极坐标系,写出圆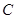 的极坐标方程;
的极坐标方程;
(2)已知直线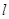 经过原点
经过原点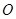 ,倾斜角
,倾斜角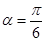 ,设
,设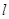 与圆
与圆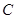 相交于
相交于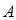 、
、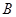 两点,求
两点,求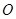 到
到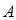 、
、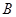 两点的距离之积。
两点的距离之积。
已知函数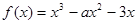
(Ⅰ)若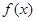 在区间上
在区间上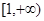 是增函数,求实数
是增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)若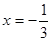 是
是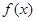 的极值点,求
的极值点,求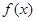 在
在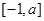 上的最大值和最小值.
上的最大值和最小值.
设函数 的所有整数值的个数为g(n) .
的所有整数值的个数为g(n) .
(1)求g(n)的表达式;
(2)设 的最小值
的最小值
(3)设
某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元
(1)设半圆的半径OA=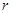 (米),试建立塑胶跑道面积S与
(米),试建立塑胶跑道面积S与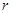 的函数关系S(
的函数关系S(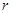 ) ,并求其定义域;
) ,并求其定义域;
(2)由于条件限制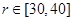 ,问当
,问当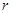 取何值时,运动场造价最低?(
取何值时,运动场造价最低?( 取3.14)
取3.14)
数列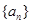 的前
的前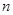 项和为
项和为 ,
,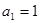 ,
,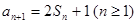 ,
,
(1)求数列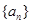 的通项公式;
的通项公式;
(2)等差数列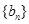 的各项为正,其前
的各项为正,其前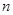 项和为
项和为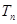 ,且
,且 ,又
,又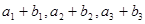 成等比数列,求
成等比数列,求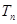 ;
;
(3)数列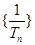 的前
的前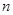 项和为
项和为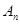 ,求
,求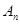 .
.