(本题满分1 3分)
3分)
某运动员进行20次射击练习,记录了他射击的有关数据,得到下表:
| 环数 |
7 |
8 |
9 |
10 |
| 命中次数 |
2 |
7 |
8 |
3 |
(Ⅰ)求此运动员射击的环数的平均数;
(Ⅱ)若将表中某一环数所对应的命中次数作为一个结果,在四个结果(2次、7次、8次、3次)中,随机取2个不同的结果作为基本事件进行研究,记这两个结果分别为 次、
次、 次,每个基本事件为(m,n).
次,每个基本事件为(m,n).
求“ ”的概率.
”的概率.
已知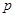 :对任意
:对任意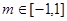 ,不等式
,不等式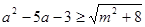 恒成立;
恒成立;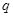 :存在
:存在 ,使不等式
,使不等式 成立,若“
成立,若“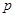 或
或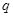 ”为真,“
”为真,“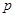 且
且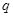 ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
在平面直角坐标系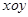 中,
中,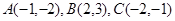 .
.
(1)求以线段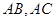 为邻边的平行四边形的两条对角线的长;
为邻边的平行四边形的两条对角线的长;
(2)设实数 满足
满足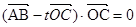 ,求
,求 的值.
的值.
(本小题满分14分)
已知数列 ,
, ,
,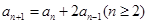
(Ⅰ)求数列 的通项公式
的通项公式 ;
;
(Ⅱ)当 时,求证:
时,求证: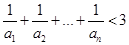
(Ⅲ)若函数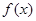 满足:
满足:
求证: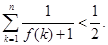
(本小题满分13分)
已知函数 .
.
(Ⅰ)求函数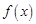 的极大值;
的极大值;
(Ⅱ)若 对满足
对满足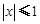 的任意实数
的任意实数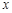 恒成立,求实数
恒成立,求实数 的取值范围(这里
的取值范围(这里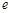 是自然对数的底数);
是自然对数的底数);
(Ⅲ)求证:对任意正数 、
、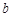 、
、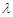 、
、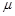 ,恒有
,恒有
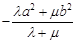 .
.
(本小题满分12分)
某工厂去年的某产品的年销售量为100万只,每只产品的销售价为10元,每只产品固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计销售量从今年开始每年比上一年增加10万只,第n次投入后,每只产品的固定成本为 (k>0,k为常数,
(k>0,k为常数, 且n≥0),若产品销售价保持不变,第n次投入后的年利润为
且n≥0),若产品销售价保持不变,第n次投入后的年利润为 万元.
万元.
(Ⅰ)求k的值,并求出 的表达式;
的表达式;
(Ⅱ)若今年是第1年,问第几年年利润最高?最高利润为多少万元?