(本小题满分10分)已知 ,
, , 且
, 且
(1) 求函数 的解析式;
的解析式;
(2) 当 时,
时,  的最小值是-4 , 求此时函数
的最小值是-4 , 求此时函数 的最大值, 并求出相应的
的最大值, 并求出相应的 的值.
的值.
已知正四棱柱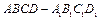 中
中 ,点E为
,点E为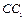 的中点,F为
的中点,F为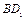 的中点。
的中点。
⑴求 与DF所成角的大小;
与DF所成角的大小;
⑵求证: 面
面 ;
;
⑶求点 到面BDE的距离。
到面BDE的距离。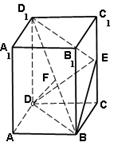
 如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,D、E分别为AC、AA1的中点.点F为棱AB上的点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,D、E分别为AC、AA1的中点.点F为棱AB上的点.
(Ⅰ)当点F为AB的中点时.
(1)求证:EF⊥AC1;
(2)求点B1到平面DEF的距离.
(Ⅱ)若二面角A-DF-E的大小为 的值.
的值.
如图,正三棱柱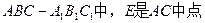 .
.
(1)求证:平面 ;
;
(2)求证: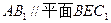 ;
;
(3)若 .
.
如图,在四棱锥P—ABCD中,底面ABCD是∠DAB=60°且边长为1的菱形。侧面PAD是正三角形,其所在侧面垂直底面ABCD,G是AD中点。
(1)求异面直线BG与PC所成的角;
(2)求点G到面PBC的距离;
(3)若E是BC边上的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并说明理由。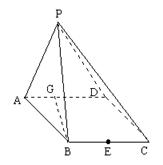
如图四棱锥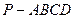 中,
中, 底面
底面 ,
, 正方形的边长为2
正方形的边长为2
(1)求点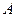 到平面
到平面 的距离;
的距离;
(2)求直线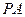 与平面
与平面 所成角的大小;
所成角的大小;
(3)求以 与
与 为半平面的二面角的正切值。
为半平面的二面角的正切值。