解关于 的不等式:
的不等式:

如图,某大风车的半径为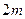 ,每
,每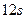 旋转一周,它的最低点
旋转一周,它的最低点
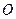 离地面
离地面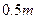 。风车圆周上一点
。风车圆周上一点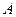 从最低点
从最低点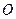 开始,运动
开始,运动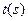 后与地面的距离为
后与地面的距离为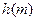 。
。
⑴求函数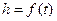 的关系式;⑵画出函数
的关系式;⑵画出函数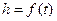 的图象。
的图象。
已知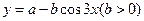 的最大值为
的最大值为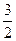 ,最小值为
,最小值为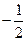 。求函数
。求函数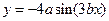 的周期、最值,并求取得最值时的
的周期、最值,并求取得最值时的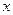 之值;并判断其奇偶性。
之值;并判断其奇偶性。
已知函数f(x)=Asin(ωx+j)的图象如图所示,试依图指出:
(1)f(x)的最小正周期;
(2)使f(x)=0的x的取值集合;
(3)使f(x)<0的x的取值集合;
(4)f(x)的单调递增区间和递减区间;
(5)求使f(x)取最小值的x的集合;
(6)图象的对称轴方程;
(7)图象的对称中心.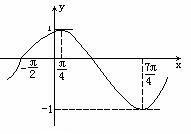
(1)化简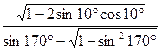 ;
;
(2)化简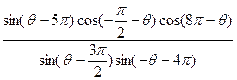
(本小题满分13分)
设M是由满足下列条件的函数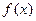 构成的集合:“①方程
构成的集合:“①方程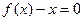 有实数根;②函数
有实数根;②函数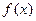 的导数
的导数 满足
满足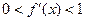 ”.
”.
(1)判断函数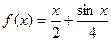 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(2)若集合M中的元素具有下面的性质:“若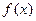 的定义域为D,则对于任意
的定义域为D,则对于任意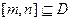 ,都存在
,都存在 ,使得等式
,使得等式 成立”,
成立”, 试用这一性质证明:方程
试用这一性质证明:方程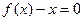 只有一个实数根;
只有一个实数根;
(3)设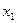 是方程
是方程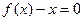 的实
的实 数根,求证:对于
数根,求证:对于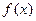 定义域中的任意的
定义域中的任意的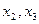 ,当
,当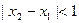 且
且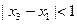 时,
时,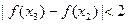 .
.