(本小题满分16分)设函数f(x)= x4+bx2+cx+d,当x=t1时,f(x)有极小值.
x4+bx2+cx+d,当x=t1时,f(x)有极小值.
(1)若b=-6时,函数f(x)有极大值,求实数c的取值范围;
(2)在(1)的条件下,若存在实数c,使函数f(x)在闭区间[m-2,m+2]上单调递增,求实数m的取值范围;
(3)若函数f(x)只有一个极值点,且存在t2∈(t1,t1+1),使f ′(t2)=0,证明:函数g(x)=f(x)- x2+t1x在区间(t1,t2)内最多有一个零点.
x2+t1x在区间(t1,t2)内最多有一个零点.
有甲、乙两个建材厂,都想投标参加某重点建设项目,为了对重点建设项目负责,政府到两建材厂抽样检查,他们从中各取等量的样品检查它们的抗拉强度指数如下:
 |
110 |
120 |
125 |
130 |
135 |
| P |
0.1 |
0.2 |
0.4 |
0.1 |
0.2 |
 |
100 |
115 |
125 |
130 |
145 |
| P |
0.1 |
0.2 |
0.4 |
0.1 |
0.2 |
其中 和
和 分别表示甲、乙两厂材料的抗拉强度,在使用时要求抗拉强度不低于120的条件下,比较甲、乙两厂材料哪一种稳定性较好.
分别表示甲、乙两厂材料的抗拉强度,在使用时要求抗拉强度不低于120的条件下,比较甲、乙两厂材料哪一种稳定性较好.
已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性的即没患病.下面是两种化验方案:
方案甲:逐个化验,直到能确定患病动物为止.
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.
(1)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;
(2)
表示依方案乙所需化验次数,求
的期望.
设随机变量 具有分布P(
具有分布P( =k)=
=k)= ,k=1,2,3,4,5,求E(
,k=1,2,3,4,5,求E( +2)2,V(2
+2)2,V(2 -1),
-1), (
( -1).
-1).
某运动员投篮时命中率p=0.6.
(1)求一次投篮命中次数 的期望与方差;
的期望与方差;
(2)求重复5次投篮时,命中次数 的期望与方差.
的期望与方差.
已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为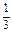 ,某植物研究所分两个小组分别独立开展该种子的发芽试验,每次试验种一粒种子,假定某次试验种子发芽,则称该次试验是成功的,如果种子没有发芽,则称该次试验是失败的.
,某植物研究所分两个小组分别独立开展该种子的发芽试验,每次试验种一粒种子,假定某次试验种子发芽,则称该次试验是成功的,如果种子没有发芽,则称该次试验是失败的.
(1)第一个小组做了三次试验,求至少两次试验成功的概率;
(2)第二个小组进行试验,到成功了4次为止,求在第四次成功之前共有三次失败,且恰有两次连续失败的概率.